16 Neuronale Netzwerke
Neuronale Netze (NN) sind leistungsstarke Modelle, die darauf spezialisiert sind, komplexe Muster in Daten zu erkennen und sind damit insbesondere ein hilfeiches Tool für Prognosen. Ein Nachteil neuronaler Netze ist die mangelnde Fähigkeit, kausale Zusammenhänge zu identifizieren und abzuleiten. Diese Limitation stellt eine signifikante Einschränkung dar, insbesondere für den Einsatz in empirischen Disziplinen, in denen das Verständnis kausaler Beziehungen von entscheidender Bedeutung ist. Während NN effektiv komplizierte Strukturen abbilden können, sind sie nicht mit den notwendigen Mechanismen ausgestattet, um Kausalität zu modellieren oder gar zu identifizieren. Grund hierfür ist die fehlende explizite Berücksichtigung kausaler Beziehungen und des zugrunde liegenden datenerzeugenden Prozesses: NN lernen lediglich funktionale Zusammenhänge in den Trainingsdaten. Auch wenn hierdurch komplexeste Relationen abgebildet werden können, erlaubt ein angepasstes Netz keine Differenzierung zwischen einer Korrelation und einer tatsächlichen kausalen Beziehung zwischen Variablen.
Weiterhin ist statistische Inferenz, etwa mit Konfidenzintervallen oder p-Werten, bei neuronalen Netzen grundsätzlich nicht wie gewohnt anwendbar: Das liegt insbesondere an der komplexen nicht-linearen Struktur und der Interaktion vieler Parameter, die schwer isoliert (und interpretiert) werden können.
In diesem Kapitel erläutern wir die Funktionsweise und Anpassung von NN und diskutieren deren Anwendung zur Prognose von Zielvariablen in Datensätzen mit vielen Variablen und Beobachtungen in R mit keras. Die hier erläuterten Grundlagen basieren auf den einleitenden Kapiteln in Bishop (2007) und Goodfellow, Bengio, und Courville (2016). Für ausführliche Erläuterungen der R-API keras für die gleichnamige Python-Bibliothek empfehlen wir Chollet und Allaire (2018).
16.1 Grundlagen und Vokabeln
NN bestehen aus einer (often großen) Anzahl so genannter künstlicher Neuronen. Ein Neuron ist eine mathematische Funktion, die mehrere Eingaben empfängt, diese unter Verwendung von Gewichten linear kombiniert und eine Ausgabe durch Verwendung einer Aktivierungsfunktion generiert.
Die Neuronen eines NN sind in Schichten (Layers) organisiert. Jedes Layer verarbeitet die Eingabedaten und gibt die Ergebnisse an das nächste Layer weiter, wobei die Neuronen verschiedener Layer miteinander verknüpft werden. Während das Eingabe-Layer (Input) die “Rohdaten” (bspw. beobachtete Regressorwerte) aufnimmt und sie an die erste versteckte Schicht (Hidden Layer) weiterleitet, ist die Hauptaufgabe der Neuronen in den Hidden Layers, komplexe Muster und Merkmale in den Daten zu erkennen und zu verarbeiten. Jedes Hidden Layer transformiert die empfangenen Daten anhand seiner Neuronen, bevor diese an das nächste Layer weitergeleitet werden. Das letzte Layer in einem neuronalen Netzwerk ist das Ausgabe-Layer (Output Layer), das die endgültige Vorhersage für die Outcome-Variable basierend auf den verarbeiteten Daten liefert.
Die Stärke der Verknüpfungen zwischen den Neuronen wird durch die Gewichte \(w\) bestimmt, welche während des Trainingsprozesses angepasst werden, um das Modell hinsichtlich der (Vorhersage) einer Zielvariable zu optimieren. Die \(w\) bestimmen, wie stark die Aktivierung eines Neurons in einer Schicht die Aktivierung der Neuronen in der nächsten Schicht beeinflusst. Das Netzwerk kann so tiefe und abstrakte Strukturen eines Datensatzes abbilden.
Angenommen wir interessieren uns für die Vorhersage einer Outcome-Variable \(Y\) mit den Regressoren \(X_1\) und \(X_2\). Abbildung 16.1 zeigt ein mögliches NN mit 3 Neuronen \(V_1\), \(V_2\), \(V_3\) in einem Hidden Layer. Die Neuronen im Hidden Layer empfangen Eingaben aus dem Input Layer, bestehend aus Beobachtungen der Variablen \(X_1\) und \(X_2\), und gewichten diese Informationen gemäß der Vorschrift
\[\begin{align*} h_i = A\left(\sum_{j=1}^{2} w_{ji} \cdot x_j + b_i\right) \quad \text{für } i = 1, 2, 3. \end{align*}\]
Hierbei sind \(w_{ji}\) die Gewichte der Verbindung von Input \(j\) zu Neuron \(i\) und \(b_i\) ist ein Bias.1 \(A(\cdot)\) ist eine Aktivierungsfunktion, die in Abhängigkeit der zu modellierenden Daten gewählt wird.
1 Der Bias ist analog zur Konstante in einer Regression.
Das Ausgabe-Neuron für \(Y\) verarbeitet die Informationen aus dem Hidden Layer ebenfalls anhand einer Linearkombination, die mit einer Aktivierungsfunktion transformiert wird,
\[\begin{align*} y = A\left(\sum_{i=1}^{3} w_{i} \cdot h_i + b_y\right). \end{align*}\]
Ein solches NN “lernt” Relationen zwischen \(Y\) und den Regressoren \(X_1\) und \(X_2\), indem die Gewichte anhand eines Algorithmus derart gewählt werden, dass der Fehler zwischen den vorhergesagten und den tatsächlichen Werten von \(Y\) — gemessen mit einer Verlustfunktion (Loss-Funktion) — minimiert wird. Dieser Lernprozess erfolgt unter Verwendung numerischer Optimierungsverfahren wie Gradientenabstieg (Gradient Descent).
16.1.1 Training Neuronaler Netze
Der Anpassungsprozess eines NN an einen Datensatz (Training) wird grob durch folgende Schritte bestimmt:
Das Netz (Gewichte) wird initialisiert.
Die Inputs jeder Beobachtung im Trainingsdatensatz werden durch das NN geleitet (Forward Pass): Jedes Layer transformiert die Daten mit Hilfe von Gewichten und Aktivierungsfunktionen, um eine Vorhersage von \(Y\) zu erzeugen.
Der Loss wird berechnet, indem die Vorhersage von \(Y\) mit dem tatsächlichen Wert verglichen wird. Die Verlustfunktion wird entsprechend der Definition von \(Y\) gewählt. Typische Verlustfunktionen sind Quadratic Loss (analog zur Schätzung von linearen Regressionsmodellen mit KQ) oder Logistic Loss (analog zu logistischer Regression).
-
Zur Anpassung der Gewichte wird der Gradient2 der Verlustfunktion hinsichtlich der Gewichte des NN ermittelt.3 Ein Gradient-Descent-Algorithmus bestimmt, in welche Richtung die Gewichte verändert werden müssen, um den Vorhersagefehler zu verringern.
Für diese Berechnung wird ein Backward Pass (auch Backpropagation genannt) genutzt. Hierbei wird der anhand des Ausgabelayers ermittelte Loss rückwärts durch das Netzwerk propagiert, um die Gewichte so anzupassen, dass der Fehler bei der Vorhersage von \(Y\) minimiert wird.
-
Die Gewichte werden in kleinen Schritten, die durch die so genannte Lernrate bestimmt werden, in Richtung des negativen Gradienten angepasst. Dies bewirkt, dass die Gewichte so verändert werden, dass der Loss im Vergleich zur letzten Iteration verringert wird.
Um den Lernprozess effizienter und stabiler zu machen, nutzen moderne Algorithmen weitere Schritte, bspw. eine Kombination von Gradientenabstieg mit Momentum. Dies beschleunigt die Anpassung der Gewichte und stabilisiert den Lernprozess. Fortgeschrittene Methoden verwenden adaptiven Lernraten, die die Schrittgröße für jedes Gewicht individuell anpassen können.
2 Der Gradient einer Funktion \(f(\boldsymbol{x}) = f(x_1, x_2, \ldots, x_k)\) ist der Vektor der partiellen Ableitungen: \(\nabla f = \left( \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \ldots, \frac{\partial f}{\partial x_k} \right)\). \(\nabla f(\boldsymbol{x})\) zeigt die Richtung und Stärke der steilsten Änderung von \(f\) am Punkt \(\boldsymbol{x}\) an.
3 \(\nabla f\) ist in NN grundsätzlich unbekannt. Gradient-Desenct-Algorithmen verwenden numerische Verfahren, um den Gradienten anhand von \(f\) zu approximieren.
Die Schritte 4 und 5 werden wiederholt, bis ein Abbruchkriterium erfüllt ist: Der Fehler ist ausreichend klein, oder weitere Iterationen bewirken keine signifikante Änderung des Gradienten.
Epochen und Iterationen
Der Gesamte Prozess wird für mehrere Epochen (Epocs) durchlaufen, in denen jeweils der gesamte Trainingsdatensatz durch das NN geleitet wird. Um das Training auch für große Datensätze durchführen zu können, werden die Trainingsdaten hierbei üblicherweise in zufällig zusammengesetzen, kleineren Datensätzen (Batches) gruppiert. In jeder Epoche erfolgt die Anpassung der Gewichte für jedes durch das Netz geleitete Batch (jede Iteration):
-
Epoche
-
Batch
Forward Pass \(\rightarrow\) Loss-Berechnung \(\rightarrow\) Backpropagation \(\rightarrow\) Gradient-Descent-Update
-
Batch
Forward Pass \(\rightarrow\) Loss-Berechnung \(\rightarrow\) Backpropagation \(\rightarrow\) Gradient-Descent-Update
…
-
-
Epoche
...…
Für das Training eines NN sind mehrere Epochen notwendig, weil ein einzelner Durchlauf der Daten oft nicht ausreicht, um die zugrundeliegenden Muster zu lernen. Durch Anpassung über mehrere Epochen können die Gewichte des Modells verfeinert werden, was insbesondere die Fähigkeit zur Generalisierung für ungesehene Daten verbessert. Die zufällige Einteilung der Daten in Batches zu Beginn jeder Epoche verhindert unter anderem, dass das NN lediglich die Reihenfolge der durchgeleiteten Datenpunkte lernt.
Die Anzahl an zu durchlaufender Epochen ist ein Tuning-Parameter: Zu wenige Epochen führen zu einer schlechten Anpassung an die Daten, während zu viele Epochen das Risiko von Overfitting erhöhen. Um den Vorhersagefehler für ungesehene Daten einzuschätzen, wird ein Testdatensatz vorbehalten. Dieser Datensatz wird während des Trainings nicht zum Anpassen der Gewichte genutzt, sondern erst nach Abschluss einer Epoche für die Berechnung der Vorhersagequalität herangezogen. So kann jeweils nach dem Durchlauf einer Epoche beurteilt werden, wie gut das Modell auf neue, unbekannte Daten generalisiert. Hierbei können ein hoher Vorhersagefehler für den Testdatensatz und ein (viel) geringerer Fehler für den Trainingsdatensatz nach mehreren Epochen auf Overfitting hinweisen. Im empirischen Teil dieses Kapitels diskutieren wir (grafische) Methoden zur Beurteilung der Anpassung des Modells.
Beim Training von NN können sogenannte Callback-Funktionen eingesetzt werden, um den Anpassungsprozess unter Einbezug von Zwischenergebnissen zu bestimmten Zeitpunkten während des Trainingsprozesses, z. B. am Ende jeder Epoche oder nach einer bestimmten Anzahl von Iterationen, zu evaluieren. Callbacks werden verwendet, um bestimmte Aktionen auszuführen, wie das Anpassen der Lernrate oder das Überwachen der Trainingsleistung: Ein Callback kann das Training automatisch stoppen (Early Stopping), wenn Anzeichen von Overfitting erkannt werden, beispielsweise wenn die Vorhersagegüte auf dem Test-Datensatz über mehrere Epochen hinweg stagniert. Dadurch wird ein unnötiges Fortsetzen des Trainings vermieden und ein Verlust der Generalisierungsfähigkeit auf neuen Daten verhindert.
Wir fassen die wichtigsten Begriffe für die Beschreibung von NN nachfolgend kurz zusammen.
Wesentliche Definitionen
Layer: Eine Ebene von Neuronen im neuronalen Netzwerk. Es gibt das Eingabe-Layer, versteckte Layers (Hidden Layers) und das Ausgabe-Layer. Jedes Layer verarbeitet Informationen aus dem vorangegangenen Layer und gibt die Ergebnisse an das nächste Layer weiter.
Input: Die Eingangsdaten oder Merkmale, die in das NN eingespeist werden. Jeder Input wird durch ein oder mehrere Neuronen im Eingabe-Layer repräsentiert.
Output: Das Ergebnis, welches das NN nach der Verarbeitung der Inputs liefert. Der Output wird durch die Neuronen im Output-Layer des NN erstellt.
Neuron: Die kleinste Komponente eines NN. Jedes Neuron empfängt Inputs, multipliziert sie mit Gewichten, addiert einen Bias und gibt das Ergebnis nach Anwendung einer Aktivierungsfunktion weiter: Ein Neuron ist also eine mathematische Funktion, die Inputs aus dem vorherigen Layer mit einer transformierten Linearkombination verarbeitet und das Ergebnis das nächste Layers weiterleitet.
Forward Pass: Leitung der Trainingsdaten durch das NN und Berechnung der Vorhersage des Outcomes.
Loss-Funktion: Mathematische Funktion, welche die Güte der Vorhersage des NN für das Outcome quantifiziert. Der Loss ist eine Funktion der zu trainierenden Parameter des NN.
Backward Pass / Backpropagation: Ermittlung des Gradienten der Loss-Funktion durch Verkettung des Effekts der Gewichte über die Layers des NN.
-
Aktivierungsfunktion: Eine mathematische Funktion, die auf die gewichtete Summe der Eingaben eines Neurons angewendet wird. Die Aktivierungsfunktion bestimmt, ob ein Neuron aktiviert wird. Beispiele sind
\[\begin{align*} \textup{ReLU}(z) =& \max(0, z), \\[.5ex] \sigma(z) =&\, \frac{1}{1 + e^{-z}}, \\[.5ex] \tanh(z) =&\, \frac{e^z - e^{-z}}{e^z + e^{-z}}. \end{align*}\]
Epoche: Ein Trainingszyklus, bei dem der gesamte Trainingsdatensatz, aufgeteilt in Batches, das NN durchläuft.
Batches: Zufällig eingeteilte Teilmengen der Beobachtungen des Trainingsdatensatzes.
Callback: Eine Funktion, die im Zuge der Überwachung des des Trainings-Prozesses automatisch ausgeführt wird, um Aktionen wie Lernratenanpassung oder Trainingsstopp zu auszulösen.
Im nächsten Abschnitt erläutern wir die Optimierung der Gewichte mit Gradient Descent beispielhaft anhand interaktiver Visualisierungen.
16.2 Optimierung mit Gradient Descent
Gradient Descent ist ein iteratives Optimierungsverfahren zur Minimierung einer differenzierbaren Zielfunktion \(f(w)\). Ausgehend von einem Startwert \(w_0\) aktualisiert der Algorithmus die Variable \(w\) schrittweise gemäß einer Lernrate \(\eta\) in die entgegengesetzte Richtung des Gradienten \(\nabla f(w)\) der Funktion an der aktuellen \(w\). Mit \(\nabla f(w)\) wird mathematisch die Richtung des steilsten Anstiegs von \(f(w)\) im Punkt \(w\) ermittelt. Der Algorithmus vollzieht eine Veränderung von \(w\) in die entgegengesetzten Richtung – die Richtung mit dem schnellsten Abstieg (Descent) der Zielfunktion.
Der folgende Algorithmus zeigt die grundlegende Vorgehensweise des Gradientenabstiegsverfahrens für einen einziegen zu optimierenden Parameter \(w\) unter Einbeziehung eines Momentum-Terms \(v_t\).4 Der Momentum-Term dient dazu, das Konvergenzverhalten zu verbessern und lokale Minima effektiver zu überwinden. Die Stärke des Momentums \(v_t\) wird durch den Momentum-Faktor \(\alpha \in [0,1)\) bestimmt.
4 In der Literatur wird \(v_t\) häufig auch als Velocity bezeichnet.
\[\begin{align*} \small & \textbf{Algorithmus: Gradientenabstiegsverfahren mit Momentum} \\ & \textup{Initialisiere: }\\[.5ex] & \quad w_0 \text{ (Startpunkt) }\\ & \quad \eta \text{ (Lernrate) }\\ & \quad \alpha \text{ (Momentum-Faktor) }\\ & \quad v_0 = 0 \text{ (Anfangsmomentum) } \\[1em] & \text{Iteriere für } t = 0, 1, 2, \dots \text{ bis Konvergenz:} \\[.5ex] & \quad \text{1. Berechne den Gradienten: } \nabla f(w_t) \\ & \quad \text{2. Aktualisiere den Momentum-Term: } v_{t+1} = \alpha v_t - \eta \nabla f(w_t) \\ & \quad \text{3. Aktualisiere die Position: } w_{t+1} = w_t + v_{t+1} \\ & \quad \text{4. Überprüfe das Abbruchkriterium } |\nabla f(w_t)| < \epsilon\text{ (für ein kleines $\epsilon>0$)} \\ \end{align*}\]
In der nachfolgenden interaktiven Visualisierung illustrieren wir die Minimierung einer univariaten Funktion \(\color{blue}{f(w_t)}\) über \(w_t\) anhand des obigen Algorithmus mit Lernrate \(\eta = .001\) und Momentum-Faktor \(\alpha = .925\).
Der Gradient\(\color{orange}{\nabla f(w_t)}\) ist hier die 1. Ableitung von \(\color{blue}{f(w_t)}\) nach \(w_t\). Die Richtung der Änderung von \(\color{blue}{f(w_t)}\) in \(w_t\) wird durch den orangenen Pfeil angezeigt. Beachte, wie sich der Gradient bei Variation des Start-Punkts mit dem Slider ändert. Während die Animation der Optimierung mit Gradient Descent läuft, zeigt der lilane Pfeil das Momentum (Velocity \(v_t\)) für Schirtt \(t\) an.5 Der Algorithmus iteriert die Schritte 1. bis 3. solange, bis das Abbruchkriterium \(|\textcolor{orange}{\nabla f(w_t)}| < \epsilon = 0.001\) erreicht ist, die Änderung in \(\color{orange}{\nabla f(w_t)}\) also hinreichend klein ist, dass ein Parameterwert \(w_t\) mit \(\color{blue}{f(w_t)}\) nahe des (globalen) Minimums von \(f\) plausibel ist.
5 Unterschiedliche Längen der Pfeile zeigen hier nicht Änderungen der tatsächlichen Beträge, sondern dienen lediglich der Interpretierbakeit der Grafik.
Folgende Eigenschaften der Optimierung mit Gradient Descent können anhand der Parameter geprüft werden:
-
Für Startpunkte mit großen Werten des Gradienten beginnt der Algorithmus mit einem starken Momentum: Der Abstieg in Richtung des negativen Gradients erfolgt also in großen Schritten, sodass die Optimierung schneller erfolgt als für Startpunkte in flachen Regionen von \(\color{blue}{f}\).
Dieser Effekt des Momentum auf den Pfad der zu optimierenden Parameter bei Gradient Descent ist vergleichbar mit dem Effekt der Schwerkraft auf eine Murmel, die auf einer hügeligen Oberfläche rollt: Anfangs gewinnt die Murmel an Geschwindigkeit und bewegt sich beschleunigt in Richtung des steilsten Gefälles. In flacheren Regionen wird die Bewegung langsamer und die Murmel kann in Tälern stecken bleiben, ähnlich wie der Optimierungsprozess in flachen Regionen von \(\color{blue}{f}\) langsamer verläuft oder gar stoppt, weil ein Abbruchkriterium erfüllt ist (geringe Änderung des Gradienten). Das Momentum hilft, auch in solchen flachen Bereichen weiter voranzukommen, indem es dem Parameterpfad eine gewisse “Trägheit” verleiht, die es ermöglicht, flache Stellen schneller zu durchqueren und die Optimierung effizienter zu gestalten.
Bei ungünstiger Wahl der Parameter konvergiert der Algorithmus nicht zum globalen Minimum, sondern stoppt im lokalen Minimum bei \(w = -0.5\). Dies unterstreicht die Notwendigkeit, die Hyperparameter Lernrate \(\eta\) und Momentum-Faktor \(\alpha\) sorgfältig zu wählen, beispielsweise indem die Modellgüte nach erfolgter Anpassung für verschiedene Parameter-Kombinationen verglichen wird.
In empirischen Anwendungen ist es für eine hohe Modellgüte eines neuronalen Netzwerks nicht unbedingt erforderlich, das globale Minimum zu finden: Viele Optimierungsprobleme weisen zahlreiche lokale Minima auf, die eine ausreichend gute Annäherung an das Optimum bieten können. Besonders bei hochdimensionalen Optimierungsproblemen mit komplexen Loss-Funktionen können diese lokalen Minima zufriedenstellende Lösungen darstellen. In einigen Fällen existiert möglicherweise kein globales Minimum, und der Algorithmus konvergiert zwangsläufig zu einem stabilen lokalen Minimum, das dennoch eine gute Performance gewährleistet. Daher kann es sinnvoller sein, Algorithmen zu verwenden, die das Erreichen einer robusten Lösung legen, anstatt strikt nach dem globalen Minimum zu suchen.
In Software-Implementierungen für Machine und Deep Learning wie tensorflow und keras werden fortgeschrittene Techniken wie Momentum Tuning oder Stochastic Gradient Descent (SGD) eingesetzt, um die Wahrscheinlichkeit zu erhöhen, dass der Algorithmus nicht in einem (ungünstigen) lokalen Minimum endet. Ein für die Anpassung von NN häufig verwendeter Algorithmus, der SGD verwendet, ist Adaptive Moment Estimation (Adam). Wir verwenden u.a. den Adam-Optimizer in den empirischen Beispielen.
In empirischen Anwendungen sind die zu lernenden Zusammenhänge komplex und damit die Anzahl der zu optimierenden Parameter eines NN häufig groß. Der oben erläuterte Algorithmus für Gradient Descent mit Momentum kann einfach auf Optimierungsprobleme mit \(k\) Parametern generalisiert werden. Dann ist \(\boldsymbol{w}_t\) ein Vektor mit \(k\) Gewichten, \(\boldsymbol{v}_{t+1}\) eine vektorwertige Funktion von \(\boldsymbol{v}_t\) und \(\nabla f(\boldsymbol{w}_t)\) mit Dimension \(k\) und \(f(\boldsymbol{w}_t)\) ist eine Oberfläche in einem \(k+1\)-dimensionalen Raum.
Die nachfolgende interaktive Grafik illustriert Gradient Descent mit Momentum für \(k=2\) zu optimierende Gewichte. Statt der Parameter des Algorithmus kann hier die Form der zu optimierenden Funktion manipuliert werden, sodass bis zu 6 Extremstellen vorliegen können. Der rote Punkt zeigt den Verlauf der Optimierung von \(\boldsymbol{w}_t\).
Die Animation verdeutlicht, dass lokale Minima insbesondere in höheren Dimensionen herausfordernd für Optimierungsalgorithmen sind: Durch Variation der Extrema lassen sich leicht Funktionen \(f(w_1,w_1)\) konstruieren, für die Gradient Descent mit den voreingestellten Parametern nicht gegen das globale Minimum konvergiert, sofern vorhanden. Ein günstiger Initialwert für \(\boldsymbol{w}_t\) kann die Wahrscheinlichkeit von Stops in lokalen Minima verringern: Grid Search Initialization wertet die Funktion über ein gleichmäßiges Gitter von Werten für \(\boldsymbol{w}_t\) aus und wählt als Startwert \(\boldsymbol{w}_{0,\textup{init}}\) den Punkt mit dem minimalen Funktionswert von \(f\) über alle Punkte im Gitter.
16.3 Funktionale Zusammenhänge lernen: Regression
Für einen leichten Einstieg in die Modellierung funktionaler Zusammenhänge durch NN mit statistischer Programmierung in R betrachten wir zunächst den einfachsten Zusammenhang zwischen einer Outcome-Variable \(Y\) und einem Regressor \(X\): Die einfache lineare Funktion \[\begin{align*} Y = w_1 X + b, \end{align*}\] wobei der Regressionskoeffizient \(w_1\) den Einfluss von \(X\) auf \(Y\) misst und \(b\) eine Konstante ist. Gemäß der Definitionen in Kapitel 16.1 kann dieser Funktionale Zusammenhang als NN ohne Hidden Layer dargestellt werden, wobei \(X\) ein Input-Neuron ist, dessen Information mit \(w_1\) gewichtet an das Output Layer mit einem einzigen Neuron für \(Y\) weitergegeben wird. Die Konstante \(b\) ist ein Bias, der als von \(X\) unabhängiger Einfluss von \(Y\) behandelt wird, vgl. Abbildung 16.2.
Für die Illustration der Schätzung des in Kapitel 16.1 dargestellten NN verwenden wir \(n=1000\) simulierte Datenpunkte gemäß der Vorschrift \[\begin{align} Y = 5 + 3 \cdot X + u \end{align}\] mit \(X\sim U[0,10]\) und \(u\sim N(0,1)\).
Für das Training von NN verwenden wir das Python-Paket keras. Hierzu muss lediglich eine lokale Python-Installation vorhanden sein.
Die in diesem Kapitel betrachteten NN sind sequentielle NN. Solche Modelle können in keras mit der Funktion keras_model_sequential() definiert werden. Die Struktur des Modells kann über eine Verkettung von Funktionen für Layers (keras::layer_dense()) und Aktivierungen (keras::layer_activation()) definiert werden.
Für die Implementierung des Modells in Abbildung 16.2 wählen wir mit units = 1 und input_shape = 1 ein Modell mit einem Neuron im Output Layer, das skalare Informationen verarbeitet. activation = 'linear' in layer_dense() führt zu der Aktivierungsfunktion \(A(x) = x\), d.h. die Ausgabe des Input Layers ist die gewichtete Summe der Eingaben plus Bias, ohne eine zusätzliche Transformation.
Attaching package: 'dplyr'The following objects are masked from 'package:stats':
filter, lagThe following objects are masked from 'package:base':
intersect, setdiff, setequal, unionlibrary(keras)
# NN für einfache Regression
model <- keras_model_sequential() %>%
layer_dense(
units = 1,
input_shape = 1,
activation = 'linear'
)
# Modell-Definition prüfen
modelModel: "sequential"
________________________________________________________________________________
Layer (type) Output Shape Param #
================================================================================
dense (Dense) (None, 1) 2
================================================================================
Total params: 2
Trainable params: 2
Non-trainable params: 0
________________________________________________________________________________Die Übersicht zeigt, dass model aus einem Layer für skalare Inputs und Outputs sowie zwei trainierbaren Parameters (\(w_1\) und \(b\)) besteht.
Bevor das im Objekt model definierte Modell trainiert werden kann, muss der Code kompiliert werden. Dieser Vorgang ist notwendig, da sämtliche Berechnungen in Python durchgeführt werden. Der Python-Code wird beim kompilieren in eine Zwischendarstellung (Bytecode) übersetzt, die dann von der Python-Interpreter-Laufzeitumgebung ausgeführt wird.6
6 Im Gegensatz zu Python ist R eine interpretierte Programmiersprache. Kompilierung von R-Ccode ist daher nicht notwendig.
Mit keras::compile() kompilieren wir das Modell und wählen als Optimierungsfunktion Adam mit einer Lernrate von \(.01\). Die Loss-Funktion wird über das Argument loss festgelegt, hier der mittlere absolute Fehler, \[\begin{align*}
\textup{MAE} = \frac{1}{n} \sum_{i=1}^{n} \lvert y_i - \widehat{y}_i\rvert.
\end{align*}\]
# Modell kompilieren
model %>%
compile(
optimizer = optimizer_adam(learning_rate = 0.01),
loss = 'mean_absolute_error'
)Die Kompilierung erfolgt meist innerhalb von Sekundenbruchteilen und geschieht in-place: Eine Zuweisung des kompilierten Modells in model ist nicht notwendig.
Um das Modell zu trainieren verwenden wir keras::fit(). Neben den (simulierten) Daten übergeben wir die Anzahl der zudurchlaufenden Epochen epocs. Über das Argument validation_split legen wir fest, dass 20% der Datensatzes zufällig ausgewählt und als Test-Datensatz für die Modell-Validierung während des Trainings genutzt werden sollen.
# Modell trainieren
history_snn <- model %>%
fit(
x = x,
y = y,
epochs = 50,
validation_split = .2
)Epoch 1/50
25/25 - 0s - loss: 23.1849 - val_loss: 21.9387 - 403ms/epoch - 16ms/step
Epoch 2/50
25/25 - 0s - loss: 21.6546 - val_loss: 20.4587 - 102ms/epoch - 4ms/step
Epoch 3/50
25/25 - 0s - loss: 20.1394 - val_loss: 18.9645 - 91ms/epoch - 4ms/step
Epoch 4/50
25/25 - 0s - loss: 18.6138 - val_loss: 17.4847 - 90ms/epoch - 4ms/step
Epoch 5/50
25/25 - 0s - loss: 17.0914 - val_loss: 16.0078 - 91ms/epoch - 4ms/step
Epoch 6/50
25/25 - 0s - loss: 15.5755 - val_loss: 14.5225 - 90ms/epoch - 4ms/step
Epoch 7/50
25/25 - 0s - loss: 14.0480 - val_loss: 13.0488 - 90ms/epoch - 4ms/step
Epoch 8/50
25/25 - 0s - loss: 12.5373 - val_loss: 11.5511 - 91ms/epoch - 4ms/step
Epoch 9/50
25/25 - 0s - loss: 11.0094 - val_loss: 10.0738 - 91ms/epoch - 4ms/step
Epoch 10/50
25/25 - 0s - loss: 9.4863 - val_loss: 8.6012 - 90ms/epoch - 4ms/step
Epoch 11/50
25/25 - 0s - loss: 7.9738 - val_loss: 7.1103 - 90ms/epoch - 4ms/step
Epoch 12/50
25/25 - 0s - loss: 6.4468 - val_loss: 5.6351 - 90ms/epoch - 4ms/step
Epoch 13/50
25/25 - 0s - loss: 4.9269 - val_loss: 4.1598 - 91ms/epoch - 4ms/step
Epoch 14/50
25/25 - 0s - loss: 3.4181 - val_loss: 2.6814 - 89ms/epoch - 4ms/step
Epoch 15/50
25/25 - 0s - loss: 1.9461 - val_loss: 1.3553 - 91ms/epoch - 4ms/step
Epoch 16/50
25/25 - 0s - loss: 0.9930 - val_loss: 0.9065 - 91ms/epoch - 4ms/step
Epoch 17/50
25/25 - 0s - loss: 0.8811 - val_loss: 0.8832 - 97ms/epoch - 4ms/step
Epoch 18/50
25/25 - 0s - loss: 0.8711 - val_loss: 0.8727 - 90ms/epoch - 4ms/step
Epoch 19/50
25/25 - 0s - loss: 0.8618 - val_loss: 0.8608 - 90ms/epoch - 4ms/step
Epoch 20/50
25/25 - 0s - loss: 0.8527 - val_loss: 0.8485 - 91ms/epoch - 4ms/step
Epoch 21/50
25/25 - 0s - loss: 0.8433 - val_loss: 0.8355 - 91ms/epoch - 4ms/step
Epoch 22/50
25/25 - 0s - loss: 0.8347 - val_loss: 0.8225 - 91ms/epoch - 4ms/step
Epoch 23/50
25/25 - 0s - loss: 0.8271 - val_loss: 0.8111 - 90ms/epoch - 4ms/step
Epoch 24/50
25/25 - 0s - loss: 0.8202 - val_loss: 0.8014 - 90ms/epoch - 4ms/step
Epoch 25/50
25/25 - 0s - loss: 0.8128 - val_loss: 0.7925 - 91ms/epoch - 4ms/step
Epoch 26/50
25/25 - 0s - loss: 0.8066 - val_loss: 0.7836 - 91ms/epoch - 4ms/step
Epoch 27/50
25/25 - 0s - loss: 0.8015 - val_loss: 0.7765 - 90ms/epoch - 4ms/step
Epoch 28/50
25/25 - 0s - loss: 0.7966 - val_loss: 0.7703 - 90ms/epoch - 4ms/step
Epoch 29/50
25/25 - 0s - loss: 0.7915 - val_loss: 0.7653 - 90ms/epoch - 4ms/step
Epoch 30/50
25/25 - 0s - loss: 0.7881 - val_loss: 0.7614 - 91ms/epoch - 4ms/step
Epoch 31/50
25/25 - 0s - loss: 0.7842 - val_loss: 0.7561 - 90ms/epoch - 4ms/step
Epoch 32/50
25/25 - 0s - loss: 0.7796 - val_loss: 0.7501 - 91ms/epoch - 4ms/step
Epoch 33/50
25/25 - 0s - loss: 0.7781 - val_loss: 0.7463 - 91ms/epoch - 4ms/step
Epoch 34/50
25/25 - 0s - loss: 0.7735 - val_loss: 0.7444 - 89ms/epoch - 4ms/step
Epoch 35/50
25/25 - 0s - loss: 0.7724 - val_loss: 0.7393 - 90ms/epoch - 4ms/step
Epoch 36/50
25/25 - 0s - loss: 0.7703 - val_loss: 0.7380 - 90ms/epoch - 4ms/step
Epoch 37/50
25/25 - 0s - loss: 0.7679 - val_loss: 0.7319 - 90ms/epoch - 4ms/step
Epoch 38/50
25/25 - 0s - loss: 0.7673 - val_loss: 0.7315 - 91ms/epoch - 4ms/step
Epoch 39/50
25/25 - 0s - loss: 0.7658 - val_loss: 0.7277 - 90ms/epoch - 4ms/step
Epoch 40/50
25/25 - 0s - loss: 0.7645 - val_loss: 0.7253 - 92ms/epoch - 4ms/step
Epoch 41/50
25/25 - 0s - loss: 0.7646 - val_loss: 0.7227 - 90ms/epoch - 4ms/step
Epoch 42/50
25/25 - 0s - loss: 0.7646 - val_loss: 0.7224 - 90ms/epoch - 4ms/step
Epoch 43/50
25/25 - 0s - loss: 0.7623 - val_loss: 0.7215 - 89ms/epoch - 4ms/step
Epoch 44/50
25/25 - 0s - loss: 0.7623 - val_loss: 0.7195 - 90ms/epoch - 4ms/step
Epoch 45/50
25/25 - 0s - loss: 0.7625 - val_loss: 0.7193 - 90ms/epoch - 4ms/step
Epoch 46/50
25/25 - 0s - loss: 0.7613 - val_loss: 0.7171 - 90ms/epoch - 4ms/step
Epoch 47/50
25/25 - 0s - loss: 0.7607 - val_loss: 0.7178 - 89ms/epoch - 4ms/step
Epoch 48/50
25/25 - 0s - loss: 0.7601 - val_loss: 0.7152 - 91ms/epoch - 4ms/step
Epoch 49/50
25/25 - 0s - loss: 0.7601 - val_loss: 0.7156 - 90ms/epoch - 4ms/step
Epoch 50/50
25/25 - 0s - loss: 0.7598 - val_loss: 0.7145 - 90ms/epoch - 4ms/stepDer Output zeigt die Enwicklung des Loss (MAE) für Vorhersagen des Trainingsdatensatzes (loss) und für den Test-Datensatz (val_loss) für alle 25 Epochen. Diese Informationen können mit plot() einfach visualisiert werden.
library(ggplot2)
library(cowplot)
library(purrr)
# Entwicklung des Loss über Epochen plotten
plot(history_snn) +
labs(
x = "Epoche",
y = "Wert der Verlustfunktion"
) +
theme_cowplot() +
theme(legend.position = "top")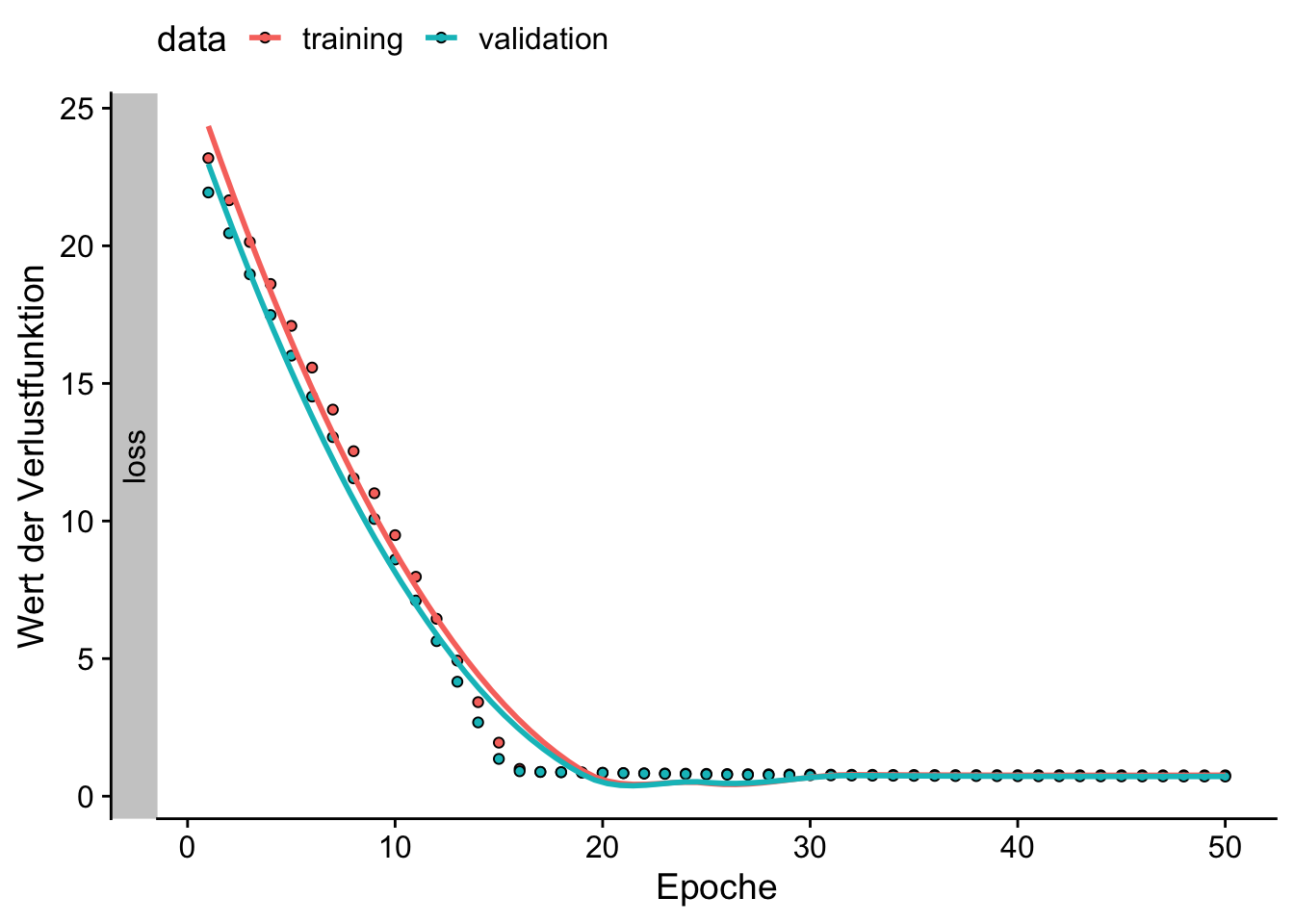
Abbildung 16.3 zeigt, dass sich sowohl die Anpassung des NN auf dem Trainingsdatenstz als auch die Generalisierung auf dem Testdatensatz innerhalb der ersten Epochen dramatisch verbessert. Jenseits der 15. Epoche hingegen bewirken weitere Trainingszyklen keine weitere Verbesserung des Loss.
Mit keras::get_weights() können wir die optimierten Parameter aus dem Modell-Objekt auslesen.
# Gewichtung und Bias des trainierten NN auslesen
model %>%
keras::get_weights() %>%
flatten_dbl() %>%
set_names(
c("w_1", "bias")
) w_1 bias
3.006937 4.935575 Das NN hat den funktionalen Zusammengang zwischen x und y erfolgreich gelernt: Die optimierten Parameter-Werte bias und w_1 liegen nahe der wahren Parameter. Bei Parameter sind mit ihren KQ-Schätzungen vergleichbar.7
7 Beachte, dass die KQ-Schätzung der Einfachheit halber hier den gesamten Datensatz nutzt und daher präziser sein kann als das NN.
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-2.91933 -0.62956 0.01084 0.63819 2.73178
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.04449 0.06028 83.69 <2e-16 ***
x 2.98893 0.01031 290.01 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9486 on 998 degrees of freedom
Multiple R-squared: 0.9883, Adjusted R-squared: 0.9883
F-statistic: 8.411e+04 on 1 and 998 DF, p-value: < 2.2e-16# Koeffizienten der KQ-Schätzung auslesen
coef(lm_model)(Intercept) x
5.044491 2.988928 Mit predict() erhalten wir Vorhersagen des NN und können so beispielsweise die Residuen für den gesamten Datensatz mit denen der KQ-Schätzung vergleichen.
# Residuen vergleichen
tibble(
NN = y - model %>% predict(x),
lm = lm_model$residuals
) %>%
ggplot(mapping = aes(x = NN, y = lm)) +
geom_point(alpha = .5, color = "steelblue") +
theme_cowplot()32/32 - 0s - 75ms/epoch - 2ms/step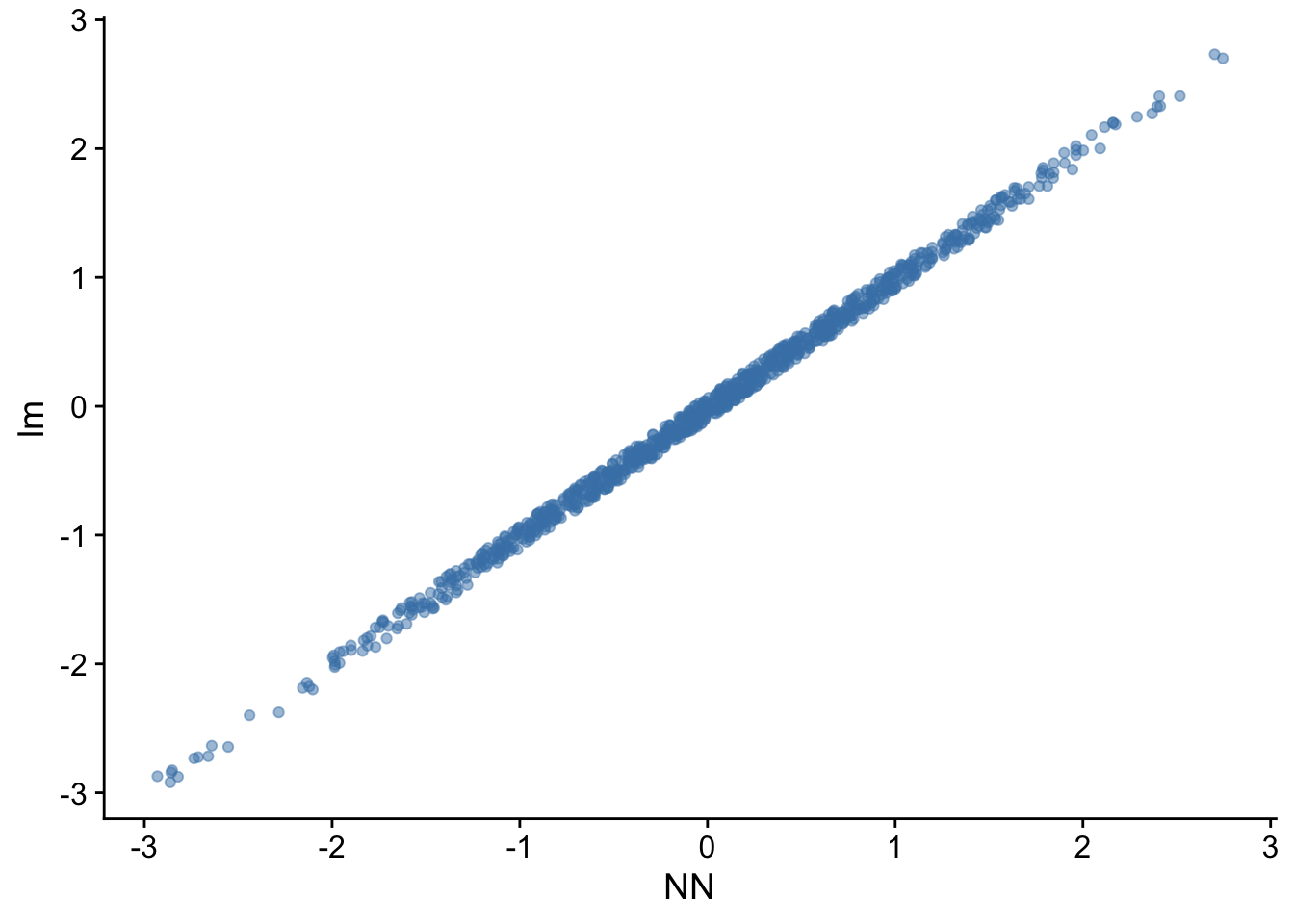
Abbildung 16.4 zeigt eine gute Korrespondenz zwischen der Anpassung des NN und der KQ-Schätzung des einfachen linearen Modells.
16.4 Multiple Regression
Ein neuronales Netz für multiple Regression kann als eine Erweiterung des Netzes für einfache Regression betrachtet werden. Das Netz enthält nun mehrere Input-Neuronen, von denen jedes eine der unabhängigen Variablen \(X_1, X_2, \dots, X_k\) repräsentiert. Diese Input-Neuronen sind mit einem einzigen Output-Neuron verbunden, das die Vorhersage für \(Y\) liefert. Jede dieser Verbindungen wird mit einem Gewicht \(w_i\) multipliziert, das die Stärke des Einflusses der jeweiligen unabhängigen Variable \(X_i\) auf die abhängige Variable \(Y\) repräsentiert. Wie im einfachen Modell gibt es einen Bias-Term \(b\), der ähnlich wie in der einen konstanten Einfluss darstellt.
Die Struktur eines NN für multiple Regression ist in Abbildung 16.5 dargestellt. In diesem Beispiel gibt es drei unabhängige Variablen \(X_1\), \(X_2\) und \(X_3\), die jeweils ein eigenes Input-Neuron haben und mit dem Output-Neuron \(Y\) verbunden sind. \(Y\) ist eine Linear-Kombination der Inputs, gewichtet mit den jeweiligen Gewichten \(w_1\), \(w_2\) und \(w_3\), sowie dem Bias \(b\).
Um die Vorgehensweise in R zu zeigen, generieren wir zunächst \(n=250\) Datenpunkte gemäß der Vorschrift \[\begin{align} Y = 5 + 3 \cdot X_1 + 2\cdot X_2 - 1.5 \cdot X_k + u \end{align}\] mit \(X_1,X_2,X_3 \sim\textup{u.i.v.} N(0, 1)\) und \(u\sim N(0,1)\).
Anschließend definieren wir ein einfaches NN und fügen ein Layer hinzu. Da wir eine multiple Regression durchführen, wählen wir input_shape = k, wobei k die Anzahl der unabhängigen Variablen ist. Wie im einfachen Modell ist die Aktivierungsfunktion linear, da wir an der Anpassung von \(Y\) mit einer linearen Kombination der Inputs interessiert sind.
# Erstellen und Kompilieren des Modells
model <- keras_model_sequential() %>%
layer_dense(
units = 1,
input_shape = k,
activation = 'linear'
)
# Modelldefinition prüfen
modelModel: "sequential_1"
________________________________________________________________________________
Layer (type) Output Shape Param #
================================================================================
dense_1 (Dense) (None, 1) 4
================================================================================
Total params: 4
Trainable params: 4
Non-trainable params: 0
________________________________________________________________________________Wir kompilieren das Modell mit dem mittleren quadratischen Fehler (mean squared error, MSE) und SGD als Loss-Funktion mit einer moderaten Lernrate.
model %>%
compile(
loss = 'mean_squared_error',
optimizer = optimizer_sgd(learning_rate = 0.01)
)Die Anpassung des Modells erfolgt wie bei einfacher Regression mit keras::fit().
# Training des Modells
history_mnn <- model %>%
fit(
x = X,
y = Y,
validation_split = .2,
epochs = 25
)Epoch 1/25
7/7 - 0s - loss: 38.3993 - val_loss: 32.8652 - 315ms/epoch - 45ms/step
Epoch 2/25
7/7 - 0s - loss: 29.4938 - val_loss: 25.0963 - 39ms/epoch - 6ms/step
Epoch 3/25
7/7 - 0s - loss: 22.4204 - val_loss: 19.6002 - 37ms/epoch - 5ms/step
Epoch 4/25
7/7 - 0s - loss: 17.4279 - val_loss: 15.4717 - 37ms/epoch - 5ms/step
Epoch 5/25
7/7 - 0s - loss: 13.6818 - val_loss: 12.2052 - 36ms/epoch - 5ms/step
Epoch 6/25
7/7 - 0s - loss: 10.7182 - val_loss: 9.5849 - 36ms/epoch - 5ms/step
Epoch 7/25
7/7 - 0s - loss: 8.3500 - val_loss: 7.6605 - 36ms/epoch - 5ms/step
Epoch 8/25
7/7 - 0s - loss: 6.6112 - val_loss: 6.2265 - 37ms/epoch - 5ms/step
Epoch 9/25
7/7 - 0s - loss: 5.3111 - val_loss: 5.0795 - 37ms/epoch - 5ms/step
Epoch 10/25
7/7 - 0s - loss: 4.2714 - val_loss: 4.2336 - 36ms/epoch - 5ms/step
Epoch 11/25
7/7 - 0s - loss: 3.4932 - val_loss: 3.6129 - 37ms/epoch - 5ms/step
Epoch 12/25
7/7 - 0s - loss: 2.9248 - val_loss: 3.1064 - 37ms/epoch - 5ms/step
Epoch 13/25
7/7 - 0s - loss: 2.4445 - val_loss: 2.7230 - 38ms/epoch - 5ms/step
Epoch 14/25
7/7 - 0s - loss: 2.0787 - val_loss: 2.4224 - 38ms/epoch - 5ms/step
Epoch 15/25
7/7 - 0s - loss: 1.7950 - val_loss: 2.2407 - 37ms/epoch - 5ms/step
Epoch 16/25
7/7 - 0s - loss: 1.6024 - val_loss: 2.0872 - 36ms/epoch - 5ms/step
Epoch 17/25
7/7 - 0s - loss: 1.4649 - val_loss: 1.9736 - 36ms/epoch - 5ms/step
Epoch 18/25
7/7 - 0s - loss: 1.3637 - val_loss: 1.9016 - 36ms/epoch - 5ms/step
Epoch 19/25
7/7 - 0s - loss: 1.2812 - val_loss: 1.8461 - 36ms/epoch - 5ms/step
Epoch 20/25
7/7 - 0s - loss: 1.2149 - val_loss: 1.8101 - 36ms/epoch - 5ms/step
Epoch 21/25
7/7 - 0s - loss: 1.1715 - val_loss: 1.7887 - 36ms/epoch - 5ms/step
Epoch 22/25
7/7 - 0s - loss: 1.1364 - val_loss: 1.7568 - 37ms/epoch - 5ms/step
Epoch 23/25
7/7 - 0s - loss: 1.1083 - val_loss: 1.7334 - 36ms/epoch - 5ms/step
Epoch 24/25
7/7 - 0s - loss: 1.0898 - val_loss: 1.7260 - 36ms/epoch - 5ms/step
Epoch 25/25
7/7 - 0s - loss: 1.0727 - val_loss: 1.7264 - 36ms/epoch - 5ms/step# Entwicklung des Loss über Epochen plotten
plot(history_mnn) +
labs(
x = "Epoche",
y = "Wert der Verlustfunktion"
) +
theme_cowplot() +
theme(legend.position = "top")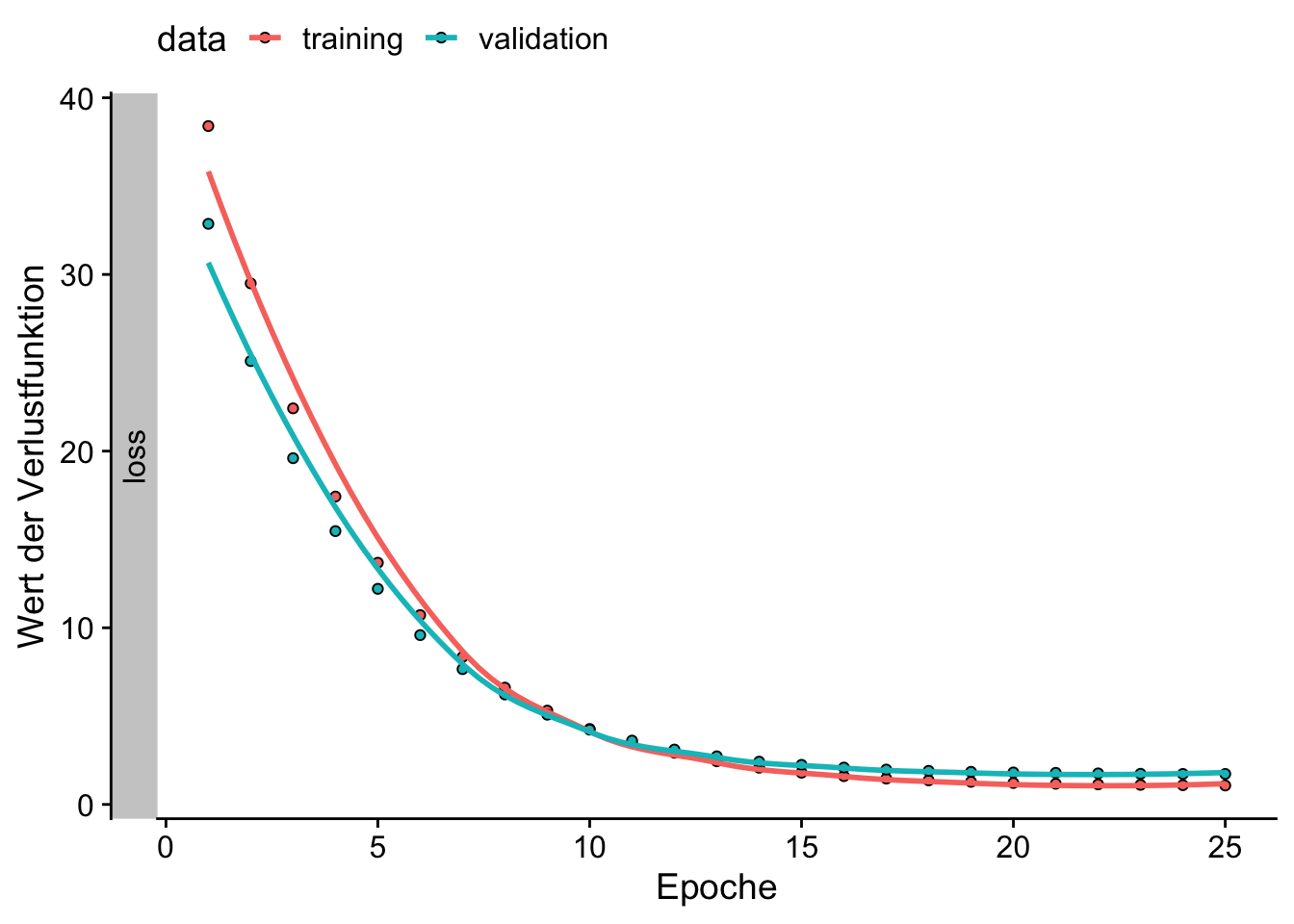
Wie bei der einfachen Regression zeigt ein Vergleich der angepassten Gewichte mit den KQ-Schätzungen eines entsprechenden linearen Regressionsmodells ähnliche Ergebnisse beider Ansätze.
# Gewichtung und Bias des trainierten NN auslesen
model %>%
keras::get_weights() %>%
flatten_dbl() %>%
set_names(
c("w_1", "w_2", "w_3", "bias")
) w_1 w_2 w_3 bias
2.945296 1.918664 -1.433969 4.803524
Call:
lm(formula = Y ~ X)
Residuals:
Min 1Q Median 3Q Max
-3.3129 -0.7286 0.0900 0.7439 3.4086
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.01583 0.06843 73.30 <2e-16 ***
X1 2.97449 0.07028 42.32 <2e-16 ***
X2 1.94345 0.07061 27.52 <2e-16 ***
X3 -1.47278 0.06914 -21.30 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.079 on 246 degrees of freedom
Multiple R-squared: 0.9271, Adjusted R-squared: 0.9262
F-statistic: 1042 on 3 and 246 DF, p-value: < 2.2e-1616.5 Nicht-Lineare Zusammenhänge
In diesem Abschnitt verwenden trainieren wir ein NN, um eine logistische Regression durchzuführen. Dieser Ansatz wird häufig verwendet, um eine binäre Outcome-Variablen \(Y\) zu modellieren, also Variablen, die zwei mögliche Ausgänge haben (oft als 0 oder 1 dargestellt), siehe Kapitel 4.2.3 für Details. Anstatt die Eingaben lediglich linear zu kombinieren, verwenden wir eine Sigmoid-Aktivierungsfunktion8, \[\begin{align*} \sigma(z) = \frac{1}{1 + \exp(-z)}, \end{align*}\] welche die Ausgaben auf einen Wertebereich zwischen 0 und 1 abbildet. Dadurch kann das NN Wahrscheinlichkeiten \(P(Y=1\vert \boldsymbol{X} = \boldsymbol{x})\) vorhersagen, die anschließend für die Klassifikation von Beobachtungen verwendet werden können.
8 Die Sigmoid-Aktivierungsfunktion entspricht der logistischen Funktion \(\Lambda(z)\) aus Kapitel 4.2.3.
Für die Illustration der Schätzung mit keras verwenden wir den DGP aus Kapitel 4.2.2.
# Erstellen von Trainingsdaten
set.seed(1234)
n <- 500
X <- rnorm(n = n, mean = 5, sd = 2) # Regressor
P <- pnorm(-4 + 0.7 * X)
Y <- as.integer(runif(n) < P)Abbildung 16.7 zeigt ein einfaches NN für eine binäre Outcome-Variable.
Nach der Definition des NN wird das Modell mit dem Binary-Cross-Entropy-Loss (BCEL) und dem Adam-Optimierer kompiliert. BCEL ist für binäre Klassifikationsprobleme geeignet: Diese Loss-Funktion misst die die Unterschiede zwischen den vorhergesagten Wahrscheinlichkeiten \(\widehat{p}_i\) und den tatsächlichen binären Zielen \(y_i\), \[\begin{align*} \textup{BCEL} = -\frac{1}{N} \sum_{i=1}^{N} \left[ y_i \cdot \log(\widehat{p}_i) + (1 - y_i) \cdot \log(1 - \widehat{p}_i) \right]. \end{align*}\] Als weitere zu berechnende Metrik wählen wir \(\textup{Accuracy}\), ein geläufiges Maß zur Bewertung der Leistung von Klassifikationsmodellen. \(\textup{Accuracy}\) gibt an, wie oft das Modell korrekte Vorhersagen getroffen hat, ausgedrückt als Verhältnis der Anzahl der korrekten Vorhersagen zur Gesamtzahl der Vorhersagen, \[\begin{align*} \text{Accuracy} = \frac{\textup{TP} + \textup{TN} }{ \textup{TP} + \textup{TN} + \textup{FP} + \textup{FN} } = \frac{\textup{Anz. korrekte Vorhersagen}}{\textup{Anz. alle Vorhersagen}}. \end{align*}\] Hierbei sind \(\textup{TP}\) und \(\textup{FP}\) die Anazhl korrekter (true positive) und falscher (false positiv) Vorhersagen für Beobachtungen mit \(y_i = 1\). \(\textup{TN}\) und \(\textup{FN}\) sind analog für Beobachtungen mit tatsächlichen Werten \(y_i = 0\) definiert.
Die Vorhersage von \(y_i\) zur Berechnung von \(\textup{Accuracy}\) erfolgt durch keras::fit() standardmäßig nach der Regel \[\begin{align*}
\hat{y}_i =
\begin{cases}
1 & \text{wenn } \hat{p}_i \geq 0.5, \\
0 & \text{wenn } \hat{p}_i < 0.5.
\end{cases}
\end{align*}\]
Wir definieren nachchfolgend das Modell-Objekt und passen das NN über 150 Epochen an.
# Erstellen und Kompilieren des Modells
model_nn_logit <- keras_model_sequential() %>%
layer_dense(
units = 1,
input_shape = 1,
activation = 'sigmoid' # <= für Logit-Modell
)
model_nn_logitModel: "sequential_2"
________________________________________________________________________________
Layer (type) Output Shape Param #
================================================================================
dense_2 (Dense) (None, 1) 2
================================================================================
Total params: 2
Trainable params: 2
Non-trainable params: 0
________________________________________________________________________________# Modell kompilieren
model_nn_logit %>%
compile(
loss = 'binary_crossentropy', # Für BCEL
optimizer = optimizer_adam(learning_rate = 0.01),
metrics = 'accuracy'
)Die Zusammenfassung der Anpassung für die letzte Epoche in history_nn_logit zeigt ergibt eine Genauigkeit von über 80% auf dem Validierungsdatensatz.
history_nn_logit
Final epoch (plot to see history):
loss: 0.4
accuracy: 0.805
val_loss: 0.3408
val_accuracy: 0.87 # Entwicklung des Loss über Epochen plotten
plot(history_nn_logit) +
labs(
x = "Epoche",
y = ""
) +
theme_cowplot() +
theme(legend.position = "top")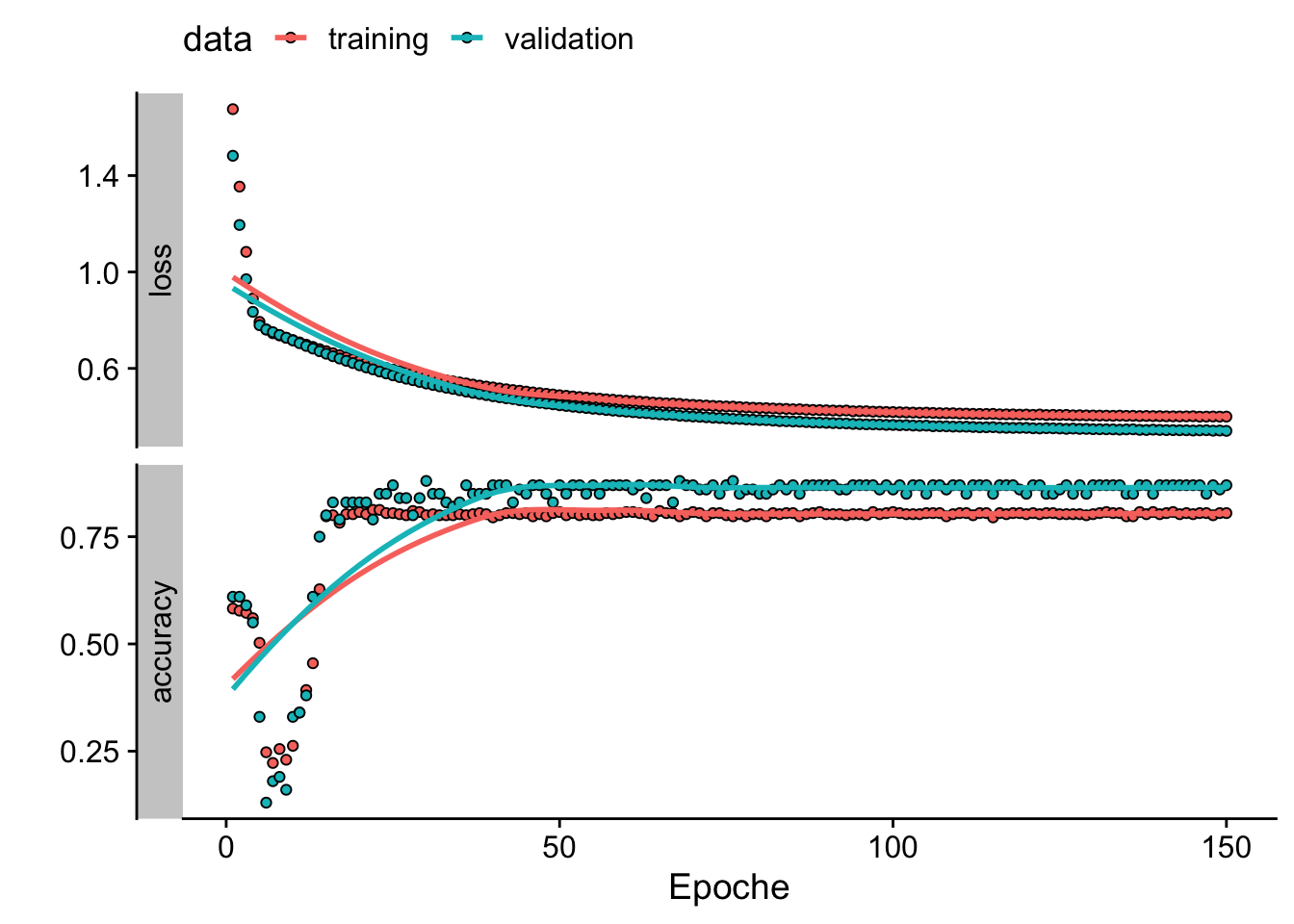
# Gewicht und Bias extrahieren
model_nn_logit %>%
keras::get_weights() %>%
flatten_dbl() %>%
set_names(
c("w_1", "bias")
) w_1 bias
0.9527357 -5.3522143 Für einen Vergleich der Vorhersagegüter mit logistischer Regression schätzen wir zunächst ein entsprechendes GLM mit glm().
# Logistisches Modell mit glm() anpassen
glm_mod <- glm(
formula = Y ~ X,
family = binomial(link = "logit")
)
summary(glm_mod)
Call:
glm(formula = Y ~ X, family = binomial(link = "logit"))
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -7.3289 0.6520 -11.24 <2e-16 ***
X 1.3140 0.1191 11.04 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 673.01 on 499 degrees of freedom
Residual deviance: 375.96 on 498 degrees of freedom
AIC: 379.96
Number of Fisher Scoring iterations: 6Wir erzeugen nun einen Testdatensatz mit 250 Beobachtungen gemäß des oben gewählten DGP.
Für die neuen Datenpunkte data_new erzeugen wir Vorhersagen von \(P(Y=1\vert X=x)\) mit model_nn_logit und glm_mod und erweitern data_new um diese.
# Vorhersagen für Trainingsdaten erstellen
predictions_nn_logit <- model_nn_logit %>%
predict(data_new$X) %>%
c()8/8 - 0s - 45ms/epoch - 6ms/steppredictions_glm_logit <- predict(
glm_mod,
newdata = data_new,
type = "response"
)
# Zusammenfassen
results <- data_new %>%
mutate(
nn_logit = predictions_nn_logit,
glm_logit = predictions_glm_logit
)
slice_head(results, n = 10)# A tibble: 10 × 5
X P Y nn_logit glm_logit
<dbl> <dbl> <int> <dbl> <dbl>
1 4.15 0.136 1 0.198 0.132
2 4.55 0.208 0 0.266 0.206
3 6.44 0.693 1 0.685 0.755
4 6.68 0.751 1 0.734 0.810
5 4.74 0.248 0 0.303 0.250
6 8.22 0.960 1 0.923 0.970
7 4.41 0.180 0 0.240 0.177
8 5.39 0.411 0 0.446 0.439
9 7.48 0.892 0 0.855 0.924
10 3.56 0.0660 0 0.124 0.0661Für eine erste Beurteilung anhand der Vorhersagen auf dem Testdatensatz plotten wir die vorhergesagten Wahrscheinlichkeiten als Funktion von X gemeinsam mit den tatsächlichen Ausprägungen der Outcome-Variable Y.
library(ggplot2)
library(cowplot)
# Plot der tatsächlichen Werte gegen die vorhergesagten Wahrscheinlichkeiten
ggplot(
data = results,
mapping = aes(x = X, y = Y)
) +
geom_point(
position = position_jitter(height = 0.05),
alpha = 0.5
) +
geom_line(
mapping = aes(y = nn_logit),
col = "darkred"
) +
geom_smooth(
method = "glm",
method.args = list(family = "binomial"),
se = FALSE
) +
labs(
title = "Logistische Regression vs. NN",
x = "x",
y = "Schätzung v. P(Y=1|X=x)"
) +
theme_cowplot()`geom_smooth()` using formula = 'y ~ x'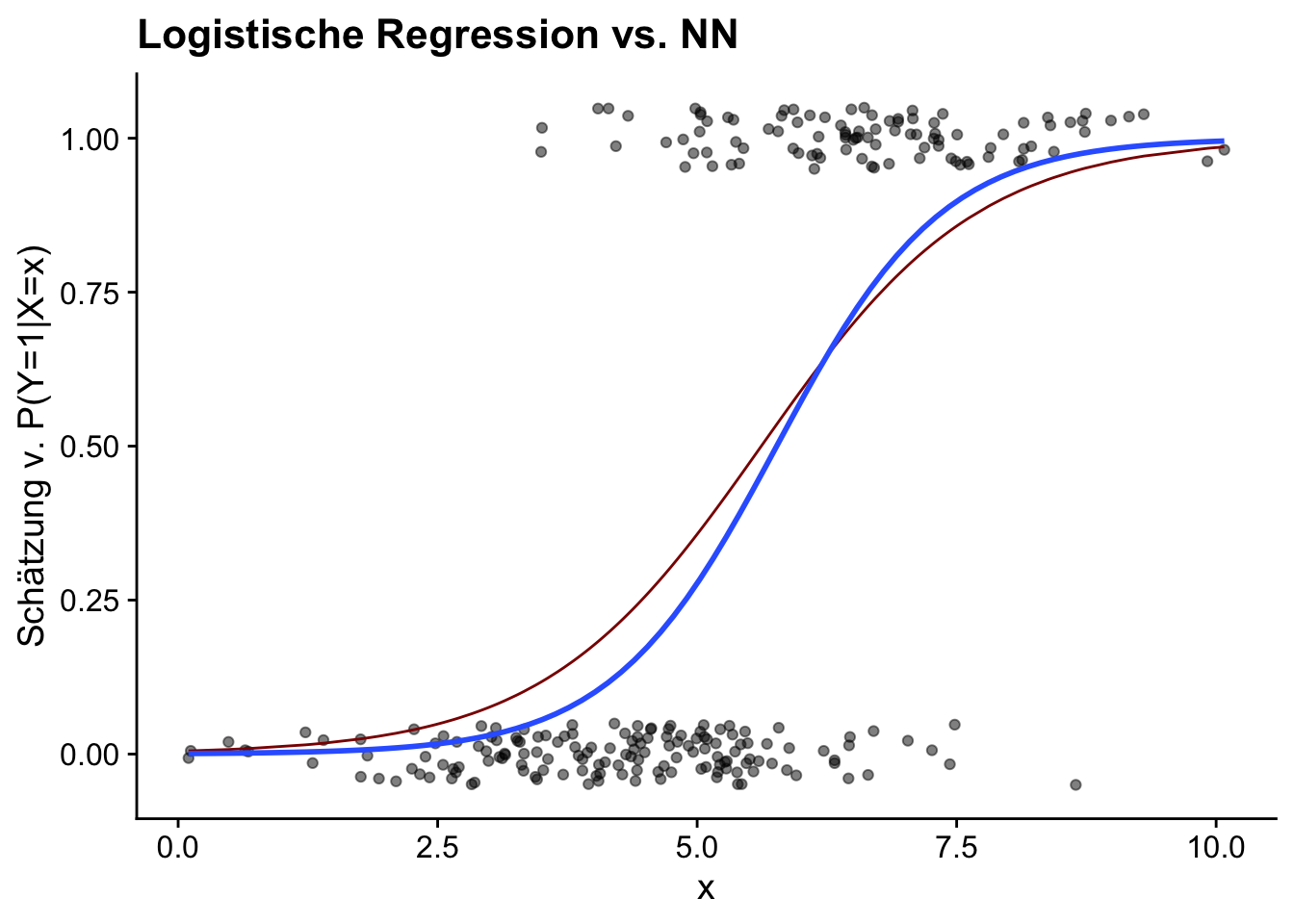
Die geschätzten Wahrscheinlichkeitsfunktionen zeigen eine gute Übereinstimmung. Um die Vorhersagegüte von model_nn_logit und model_glm_logit genauer zu untersuchen, erstellen wir Plots der jeweilgen Receiver Operating Characteristic (ROC). ROC zeigt den Zusammenhang zwischen der True Positive Rate (TPR), dem Anteil korrekter Vorhersagen für \(y_i=1\) (auch Sensitivität gennant) und der False Positive Rate (FPR), dem Anteil falscher Vorhersagen für \(y_i=1\) in Abhängigkeit des Schwellenwerts von \(\widehat{p}\) für die Klassifikation des Outcomes einer Beobachtung \(y_i = 1\). Es gilt
\[\begin{align*} TPR =&\, \frac{TP}{TP + FN},\\ \\ FPR =&\, \frac{FP}{FP + TN}. \end{align*}\]
Der Schwellenwert \(\widehat{p}\) reguliert den Trade-Off zwischen \(\textup{FPR}\) und \(\textup{TPR}\): Kleine \(\widehat{p}\) führen tendenziell zu großer \(\textup{TPR}\) (gut), aber auch zu großer \(\textup{FPR}\) (schlecht). Für ein Modell, das zufällig klassifiziert, entspricht die ROC-Kurve der Winkelhalbierenden. Wünschenwert ist ein verlauf der ROC-Kurve möglichst oberhalb der Winkelhalbierenden.
Eine ROC-Kurve kann in R mit dem plotROC anhand der Vorhergesagten und tatsächlichen Werte der Outcome-Varibale berechnet und geplottet werden. Hierzu transformieren wir results in langes Format und verwenden ggplot() mit dem Layer geom_roc().
library(plotROC)
library(tidyr)
roc_data <- results %>%
pivot_longer(
cols = glm_logit:nn_logit,
names_to = "model",
values_to = "pp"
)
# ROC-Kurve plotten
ggplot(
data = roc_data,
mapping = aes(
m = pp,
d = Y,
colour = model
)
) +
geom_roc() +
style_roc() +
facet_wrap(~ model) +
theme(legend.position = "top")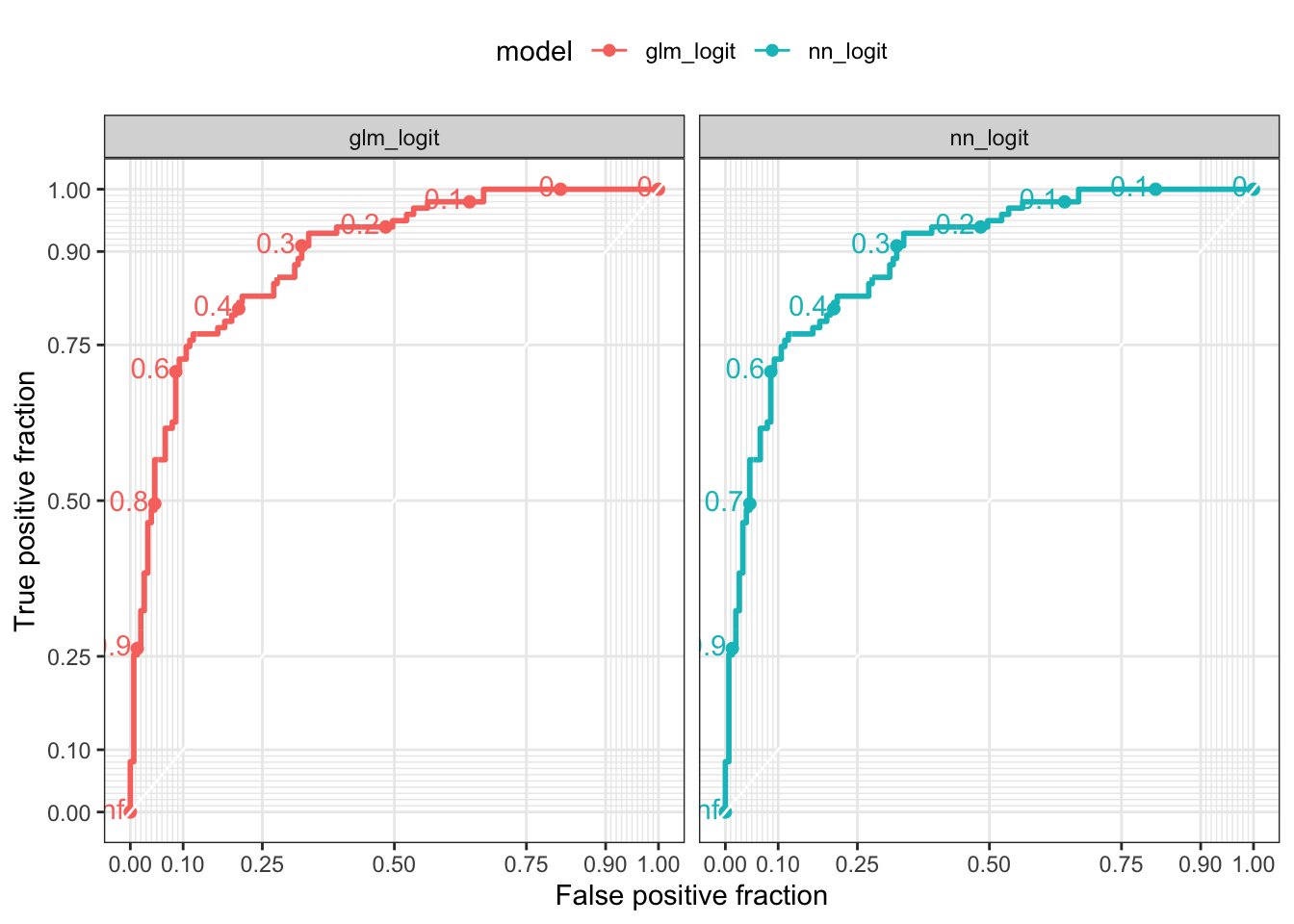
Abbildung 16.9 zeigt sehr ähnliche ROC-Kurven für model_nn_logit und model_glm_logit.9 Für die Quantifizierung der Vorhersageleistung wird Area under the Curve (AUC), die Fläche unterhalb der ROC-Kurve, herangezogen. Mit plotROC::calc_auc() kann AUC aus dem geom_roc()-Layer berechnet werden. Für ein geschätztes Modell \(\widehat{M}\) gilt \(0\leq\textup{AUC}(\widehat{M})\leq1\).10
9 Beide Plots enthalten Indikatoren des ROC für bestimmte Schwellenwerte \(\widehat{p}\).
10 Ein geschätzes, dass nicht besser als raten ist, gilt \(\textup{AUC}(\widehat{M})=.5\).
# AUC berechnen
roc_data %>%
group_by(model) %>%
summarise(
AUC = calc_auc(
ggplot(mapping = aes(m = pp, d = Y)) +
geom_roc()
)$AUC
)# A tibble: 2 × 2
model AUC
<chr> <dbl>
1 glm_logit 0.890
2 nn_logit 0.890Der Vergleich der AUC-Statistiken beider Modelle für den Testdatensatz zeigt, dass das NN ähnlich gut klassifizert, wie das GLM mit logistischer Link-Funktion.
16.6 Empirisches Beispiel: Boston Housing
In diesem Beispiel illustrieren wir die Anwendung von (NN) für den Boston Housing-Datensatz MASS::Boston. Boston enthält enthält verschiedene Charakteristika von Häusern in Boston, wie z.B. Kriminalitätsrate, Anzahl der Räume und Alter der Gebäude. Ziel ist esm den Medianpreis der Häuser (medv) vorherzusagen.
Für die Analyse verwenden wir insbesondere die Pakete tidymodels und recipes. Das recipes-Paket erlaubt eine automatisierte und leicht reproduzierbare Vorbereitung von Datensätzen für statistische Modellierung mit tidymodels. Es stellt Verben zur Konstruktion von Pipelines mit Schritten wie Skalierung, Kodierung und Handling fehlender Werte bereit. Diese Schritte werden mit einem Rezept (recipe()) definiert, vorbereitet (prep()) und dann auf Trainings- und/oder Testdaten angewendet (bake()).
Zunächst laden wir den Boston Housing-Datensatz und teilen boston_tbl in Trainings- und Testdaten auf. Hierbei verwenden wir 80% der Daten für das Training und reservieren 20% zum Testen.
── Attaching packages ────────────────────────────────────── tidymodels 1.2.0 ──✔ broom 1.0.6 ✔ rsample 1.2.1
✔ dials 1.3.0 ✔ tibble 3.2.1
✔ infer 1.0.7 ✔ tune 1.2.1
✔ modeldata 1.4.0 ✔ workflows 1.1.4
✔ parsnip 1.2.1 ✔ workflowsets 1.1.0
✔ recipes 1.0.10 ✔ yardstick 1.3.1 Warning: package 'broom' was built under R version 4.3.3Warning: package 'modeldata' was built under R version 4.3.3── Conflicts ───────────────────────────────────────── tidymodels_conflicts() ──
✖ scales::discard() masks purrr::discard()
✖ dplyr::filter() masks stats::filter()
✖ yardstick::get_weights() masks keras::get_weights()
✖ dplyr::lag() masks stats::lag()
✖ recipes::step() masks stats::step()
• Use suppressPackageStartupMessages() to eliminate package startup messages# Datensatz in tibble umwandeln
boston_tbl <- as_tibble(MASS::Boston)
# Trainings- und Testdaten einteilen
# (80% / 20%)
set.seed(1234)
split <- initial_split(boston_tbl, prop = 0.8)
train_data <- training(split)
test_data <- testing(split)
# Zielvariable und Prädiktoren aufteilen
train_x <- select(train_data, -medv)
train_y <- train_data$medv
test_x <- select(test_data, -medv)
test_y <- test_data$medvDa neuronale Netze empfindlich auf unterschiedlich skalierte Eingabedaten reagieren (ähnlich wie regularisierte Schätzer, vgl. Kapitel 13), normalisieren wir sämtliche (numerischen) Prädiktoren, ausgenommen chas und rad, mit recipes::step_normalize().
# Daten normalisieren
# Rezept
recipe_obj <- recipe(
formula = medv ~ .,
data = train_data
) %>%
step_normalize(
all_predictors(), -chas, -rad
)
# Vorbreiten
data_prep <- prep(
x = recipe_obj,
training = train_data
)
# Anwenden
train_x <- bake(
object = data_prep,
new_data = train_data
) %>%
select(-medv)
test_x <- bake(
object = data_prep,
new_data = test_data) %>%
select(-medv)Zunächst führen wir eine KQ-Regression durch, um den Zusammenhang zwischen sämtlichen verfügbaren Prädiktoren und dem Zielwert medv zu schätzen. Hierfür nutzen wir das linear_reg()-Modell aus tidymodels und passen es mit der Methode der kleinsten Quadrate (KQ) an.
Für das NN wählen wir eine Spezifikation mit zwei Hidden Layers, die jeweils 64 Neuronen haben. Mit input_shape = ncol(train_x) verarbeitet das 1. Hidden Layer die Inputs sämtlicher Prädiktoren in boston_tbl. Als Aktivierungsfunktion verwenden wir Recified Linear Unit, \[\begin{align}
\textup{ReLU}(z) \max(0, z).\\
\end{align}\]
Die ReLU-Aktivierungsfunktion setzt also negative Werte auf 0 und lässt positive Werte unverändert. In NN ermöglicht sie eine sparsame anpassung und ist numerisch leicht handhabbar bei der Berechnung des Gradienten: Die Verwendung von Layers mit ReLU verringert das Vanishing-Gradient-Problem.11
11 Bei nicht-linearen Aktivierungsfunktionen kann der Gradient der Loss-Funktion extrem klein werden, was das Training von NN mit vielen Layers schwierig machen kann.
Das Output Layer des Netzes besteht aus einem einzigen Neuron, dass einen numerischen Wert (den geschätzten Hauspreis) zurückgibt.
# NN mit Keras erstellen
model <- keras_model_sequential() %>%
# Hidden Layer 1
layer_dense(
units = 64,
activation = "relu",
input_shape = ncol(train_x)
) %>%
# Hidden Layer 2
layer_dense(
units = 64,
activation = "relu"
) %>%
# Output Layer
layer_dense(units = 1)
# Modell kompilieren
model %>% compile(
optimizer = "rmsprop",
loss = "mse",
metrics = "mae"
)Wir trainieren das NN über 100 Epochen mit einem Batch-Größe von 32 Datenpunkten.
Mit dem trainierten Nachdem das NN trainiert ist, verwenden wir model, um Vorhersagen auf den Testdaten test_data zu machen.
4/4 - 0s - 65ms/epoch - 16ms/stepUm die Leistung der Modelle zu vergleichen, berechnen wir den MSE für beide Modelle.
# MSE berechnen
ols_mse <- kq_predictions %>%
summarise(mse = mean((medv - kq_pred)^2)) %>%
pull(mse)
nn_mse <- nn_predictions %>%
summarise(mse = mean((medv - nn_pred)^2)) %>%
pull(mse)
c(
"MSE KQ" = ols_mse,
"MSE NN" = nn_mse
) MSE KQ MSE NN
28.79773 10.82384 Da das NN ist in der Lage ist, nicht-lineare Zusammenhänge zwischen den Prädiktoren und der Zielvariablen zu modellieren, liefert hat es eine höhere Vorhersagegenauigkeit auf dem Testdatensatz.
Für eine Visualisierung der Vorhersagen tragen wir den wahren und die vorhergesagten Werte von medv für beide Modelle in einem Punkteplot ab.
# KQ- und NN-Vorhersagen sammeln
preds <- kq_predictions %>%
select(medv, kq_pred) %>%
mutate(nn_pred = nn_predictions$nn_pred)
# Visualisierung der Ergebnisse mit ggplot2
preds %>%
ggplot(aes(x = medv)) +
geom_point(aes(y = kq_pred, color = "OLS"), alpha = 0.6) +
geom_point(aes(y = nn_pred, color = "Neuronales Netz"), alpha = 0.6) +
geom_abline(intercept = 0, slope = 1, linetype = "dashed") +
labs(
x = "Wahre Werte (medv)",
y = "Vorhersagen",
color = "Modell"
) +
theme_minimal() +
scale_color_manual(
values = c(
"OLS" = "red",
"Neuronales Netz" = "steelblue"
)
)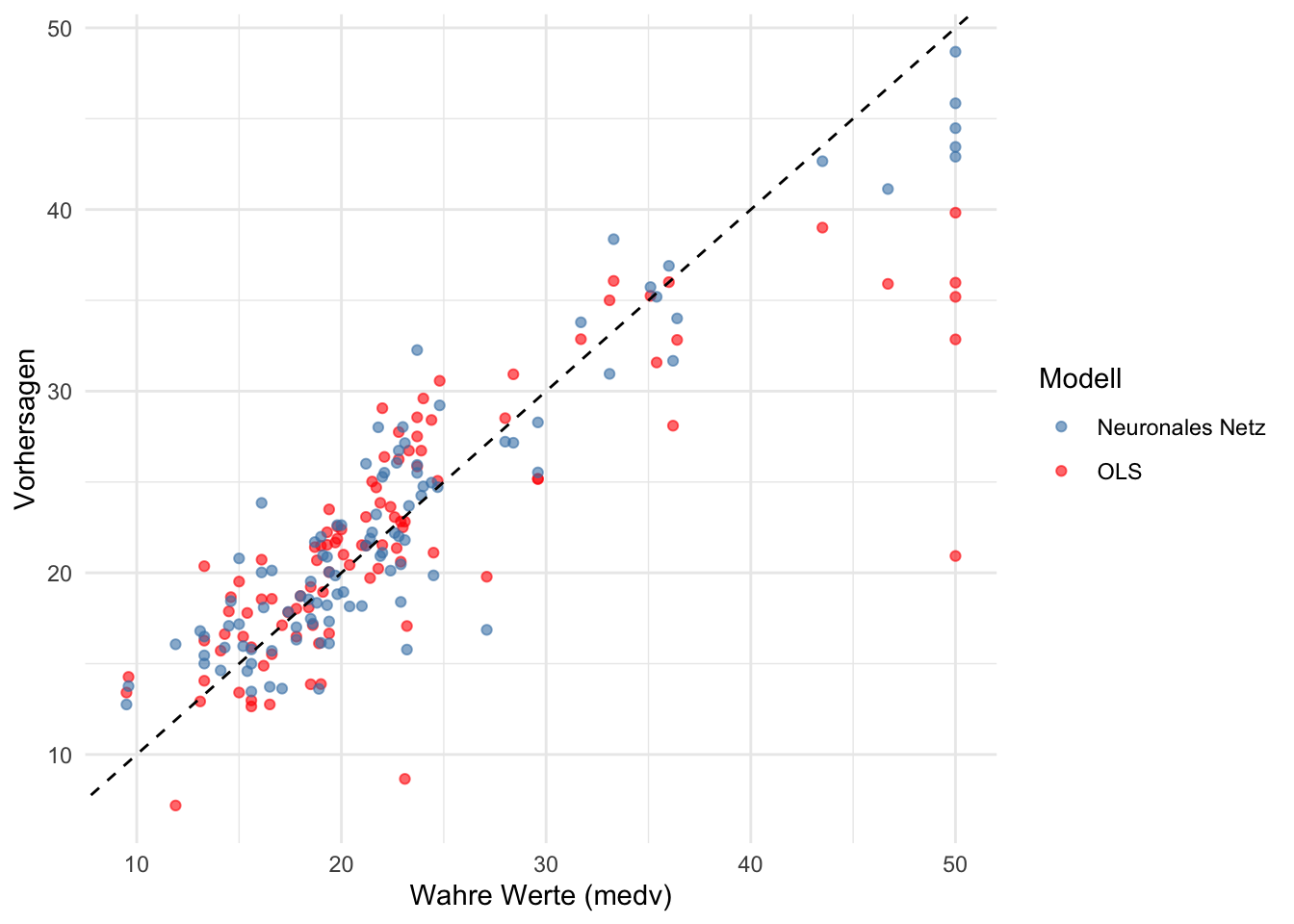
Abbildung 16.10 zeigt, dass KQ und NN weitgehend vergleichbare Vorhersagen von medv auf dem Testdatensatz liefern. Das NN scheint jedoch im Mittel besser in der Vorhersage hoher Verkaufspreise zu sein – möglicherweise weil extreme Preise auf nicht-lineare Beziehungen zwischen bestimmten Regressoren und medv zurückzuführen sind, die in einer linearen KQ-Regression nicht erfasst werden können.
16.7 Case Study: Vorhersage von Immobilienpreisen
library(AmesHousing)
housing <- make_ames()Linking to GEOS 3.11.0, GDAL 3.5.3, PROJ 9.1.0; sf_use_s2() is TRUETo enable caching of data, set `options(tigris_use_cache = TRUE)`
in your R script or .Rprofile.# Retrieve basemap for Ames, Iowa using the tigris package
places_map <- places(
state = 'IA',
cb = TRUE,
progress = F
) %>%
st_as_sf()Retrieving data for the year 2022# Filter for Ames city
ames_map <- places_map %>%
filter(NAME == "Ames")
houses <- housing %>%
select(Latitude, Longitude, Sale_Price) %>%
mutate(
Sale_Price = cut(log(Sale_Price, base = 2), breaks = 5, labels = FALSE)
) %>%
st_as_sf(coords = c("Longitude", "Latitude"),
crs = 4326, agr = "constant")
rainbow_colors <- rainbow(5, rev = TRUE)# Plot the map with just the outline of Ames
ggplot() +
geom_sf(data = ames_map, color = "black", fill = alpha("black", alpha = 0)) +
geom_sf(data = houses, mapping = aes(color = factor(Sale_Price)), size = .2) +
theme_map() +
scale_color_manual(
name = "log(Verkaufspreis)",
values = rainbow_colors,
labels = levels(factor(houses$Sale_Price))
) +
theme(legend.position = "bottom", legend.direction = "horizontal") +
ggtitle("Verkaufte Häuser in Ames, Iowa")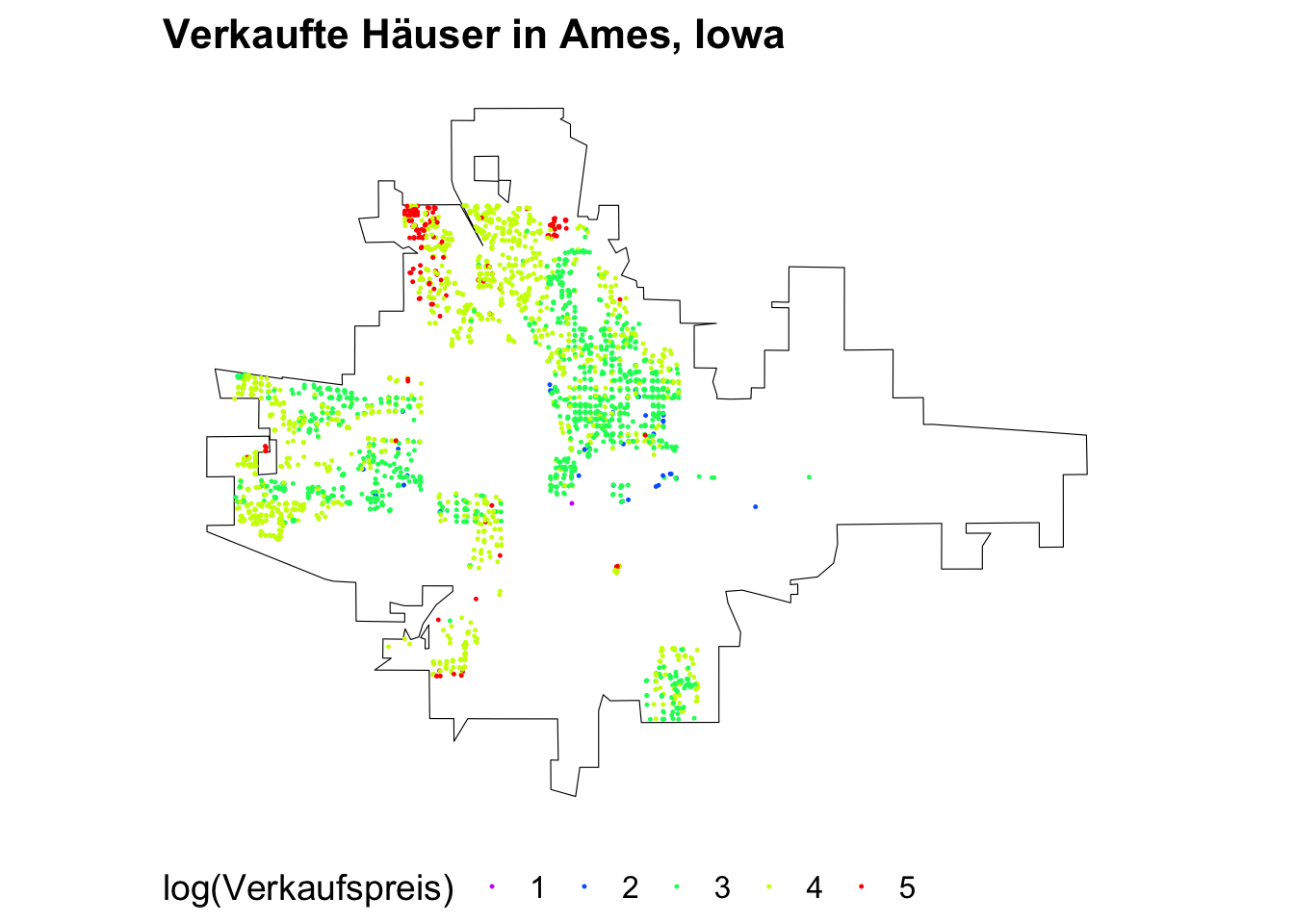
housing %>%
ggplot(mapping = aes(x = Year_Built, y = Sale_Price)) +
geom_point(alpha = .5, fill = "steelblue") +
theme_cowplot()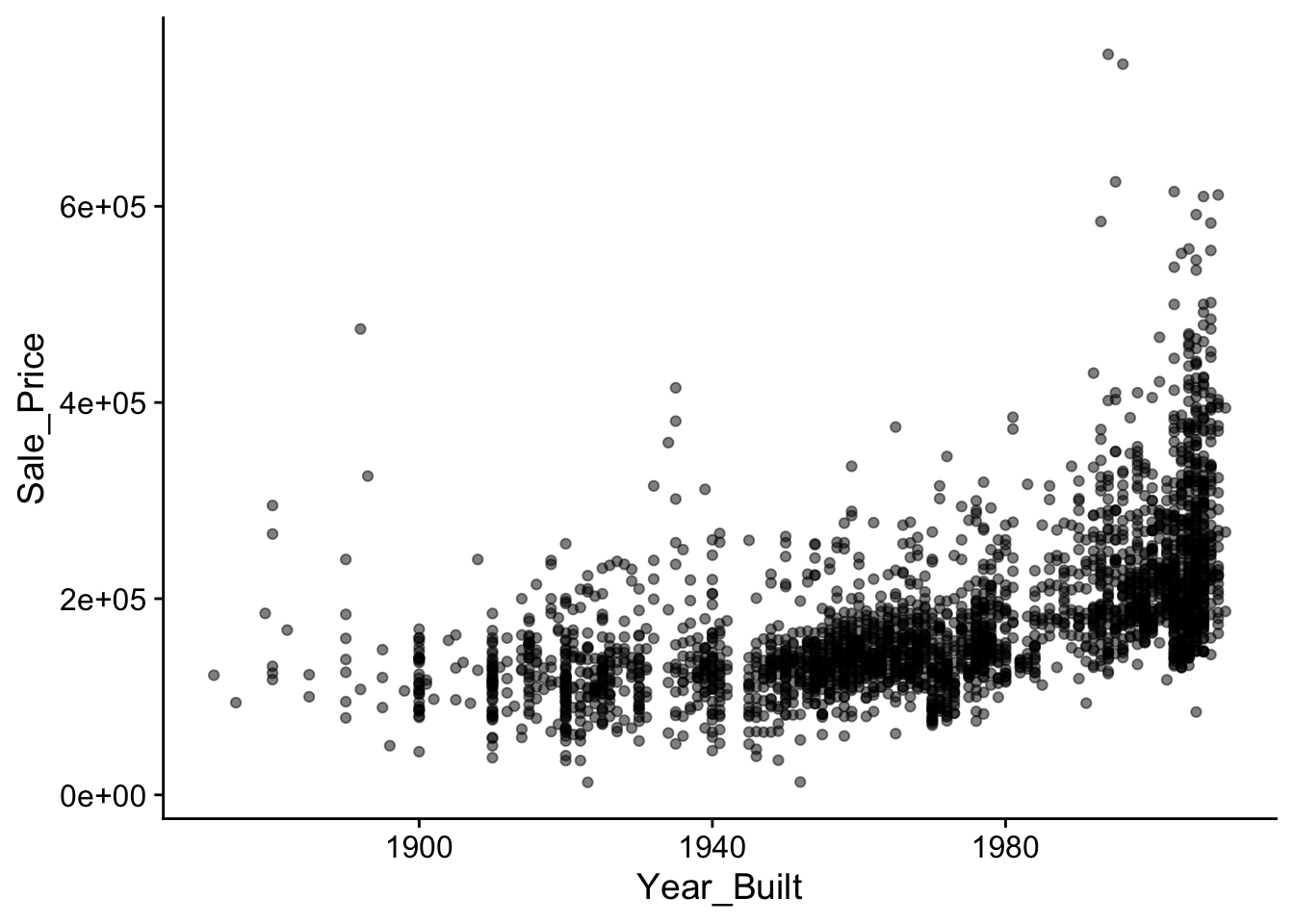
# Split the data into training and testing sets
set.seed(1234)
library(tidymodels)
split <- initial_split(housing, prop = 0.8)
housing_train <- training(split)
housing_test <- testing(split)
# Separate the predictors and the outcome
housing_train_x <- housing_train %>% select(-Sale_Price)
housing_train_y <- housing_train$Sale_Price
housing_test_x <- housing_test %>% select(-Sale_Price)
housing_test_y <- housing_test$Sale_Priceblueprint <- recipe(
Sale_Price ~ .,
data = housing_train) %>%
step_nzv(all_nominal()) %>%
step_other(all_nominal(), threshold = .01, other = "other") %>%
step_integer(matches("(Qual|Cond|QC|Qu)$")) %>%
step_YeoJohnson(all_numeric(), -all_outcomes()) %>%
step_center(all_numeric(), -all_outcomes()) %>%
step_scale(all_numeric(), -all_outcomes()) %>%
step_dummy(all_nominal(), -all_outcomes(), one_hot = TRUE)
prepare <- prep(blueprint, training = housing_train)
prepare── Recipe ──────────────────────────────────────────────────────────────────────── Inputs Number of variables by roleoutcome: 1
predictor: 80── Training information Training data contained 2344 data points and no incomplete rows.── Operations • Sparse, unbalanced variable filter removed: Street and Alley, ... | Trained• Collapsing factor levels for: MS_SubClass and MS_Zoning, ... | Trained• Integer encoding for: Overall_Qual and Overall_Cond, ... | Trained• Yeo-Johnson transformation on: Lot_Frontage and Lot_Area, ... | Trained• Centering for: Lot_Frontage, Lot_Area, Overall_Qual, ... | Trained• Scaling for: Lot_Frontage, Lot_Area, Overall_Qual, ... | Trained• Dummy variables from: MS_SubClass, MS_Zoning, Lot_Shape, ... | Trainedbaked_train <- bake(prepare, new_data = housing_train)
baked_test <- bake(prepare, new_data = housing_test)
baked_train# A tibble: 2,344 × 190
Lot_Frontage Lot_Area Overall_Qual Overall_Cond Year_Built Year_Remod_Add
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1.15 0.350 -0.0340 -0.487 0.843 0.654
2 0.277 -0.0336 -0.800 -0.487 -0.155 -0.839
3 -0.129 -0.0213 -0.800 -1.76 -1.75 -1.66
4 -0.909 -3.19 -0.0340 0.479 0.277 0.365
5 0.407 -0.223 -1.68 1.26 -0.0554 -0.694
6 -1.88 0.0595 1.28 -0.487 1.01 0.847
7 0.407 0.000506 0.655 -0.487 0.943 0.750
8 0.144 -0.377 -0.0340 -0.487 0.910 0.895
9 -0.0461 -1.52 -0.0340 -0.487 0.111 -0.453
10 1.98 0.501 1.28 -0.487 0.876 0.654
# ℹ 2,334 more rows
# ℹ 184 more variables: Mas_Vnr_Area <dbl>, Exter_Qual <dbl>, Exter_Cond <dbl>,
# Bsmt_Qual <dbl>, BsmtFin_SF_1 <dbl>, BsmtFin_SF_2 <dbl>, Bsmt_Unf_SF <dbl>,
# Total_Bsmt_SF <dbl>, Heating_QC <dbl>, First_Flr_SF <dbl>,
# Second_Flr_SF <dbl>, Low_Qual_Fin_SF <dbl>, Gr_Liv_Area <dbl>,
# Bsmt_Full_Bath <dbl>, Bsmt_Half_Bath <dbl>, Full_Bath <dbl>,
# Half_Bath <dbl>, Bedroom_AbvGr <dbl>, Kitchen_AbvGr <dbl>, …Loading required package: Matrix
Attaching package: 'Matrix'The following objects are masked from 'package:tidyr':
expand, pack, unpackLoaded glmnet 4.1-8# Prepare the data for glmnet (which requires matrices)
x_train_glmnet <- as.matrix(baked_train %>% select(-Sale_Price))
y_train_glmnet <- log10(baked_train$Sale_Price)
x_test_glmnet <- as.matrix(baked_test %>% select(-Sale_Price))
# Fit a Ridge Regression model
ridge_model <- glmnet(x_train_glmnet, y_train_glmnet, alpha = 0)
# Use cross-validation to find the optimal lambda
cv_ridge <- cv.glmnet(x_train_glmnet, y_train_glmnet, alpha = 0)
best_lambda <- cv_ridge$lambda.min
# Predict on the test set using the best lambda
ridge_preds_log <- predict(cv_ridge, s = best_lambda, newx = x_test_glmnet)
# Convert predictions back from log scale
ridge_preds <- as.numeric(10^ridge_preds_log)
# Evaluate the performance
mae_vec(
truth = housing_test_y,
estimate = ridge_preds
)[1] 14695.86x_train <- select(baked_train, -Sale_Price) %>% as.matrix()
y_train <- baked_train %>% pull(Sale_Price)
x_test <- select(baked_test, -Sale_Price) %>% as.matrix()
y_test <- baked_test %>% pull(Sale_Price)
network <- keras_model_sequential() %>%
layer_dense(units = 512, activation = "relu", input_shape = ncol(x_train)) %>%
layer_dense(units = 512, activation = "relu") %>%
layer_dense(units = 512, activation = "relu") %>%
layer_dense(units = 512, activation = "relu") %>%
layer_dense(units = 512, activation = "relu") %>%
layer_dense(units = 1)
network %>%
compile(
optimizer = optimizer_rmsprop(learning_rate = 0.01),
loss = "msle",
metrics = c("mae")
)
set.seed(1234)
history <- network %>% fit(
x_train,
y_train,
epochs = 30,
batch_size = 32,
validation_split = 0.2,
callbacks = list(
callback_early_stopping(patience = 10, restore_best_weights = TRUE),
callback_reduce_lr_on_plateau(factor = 0.2, patience = 4)
)
)Epoch 1/30
59/59 - 2s - loss: 2.6961 - mae: 65566.8516 - val_loss: 0.1204 - val_mae: 61695.5000 - lr: 0.0100 - 2s/epoch - 29ms/step
Epoch 2/30
59/59 - 1s - loss: 0.3329 - mae: 103204.2891 - val_loss: 0.3089 - val_mae: 77835.7578 - lr: 0.0100 - 571ms/epoch - 10ms/step
Epoch 3/30
59/59 - 1s - loss: 0.2295 - mae: 79307.1562 - val_loss: 0.0469 - val_mae: 31878.8457 - lr: 0.0100 - 596ms/epoch - 10ms/step
Epoch 4/30
59/59 - 1s - loss: 0.1750 - mae: 69237.9922 - val_loss: 0.0602 - val_mae: 37176.0469 - lr: 0.0100 - 572ms/epoch - 10ms/step
Epoch 5/30
59/59 - 1s - loss: 0.1273 - mae: 57111.7969 - val_loss: 0.0546 - val_mae: 39749.2852 - lr: 0.0100 - 569ms/epoch - 10ms/step
Epoch 6/30
59/59 - 1s - loss: 0.1003 - mae: 47636.3320 - val_loss: 0.1183 - val_mae: 55252.9570 - lr: 0.0100 - 563ms/epoch - 10ms/step
Epoch 7/30
59/59 - 1s - loss: 0.0913 - mae: 47773.8320 - val_loss: 0.0235 - val_mae: 17547.1543 - lr: 0.0100 - 565ms/epoch - 10ms/step
Epoch 8/30
59/59 - 1s - loss: 0.0786 - mae: 38930.9961 - val_loss: 0.0226 - val_mae: 18443.8047 - lr: 0.0100 - 571ms/epoch - 10ms/step
Epoch 9/30
59/59 - 1s - loss: 0.0717 - mae: 40277.1797 - val_loss: 0.0743 - val_mae: 41584.4727 - lr: 0.0100 - 600ms/epoch - 10ms/step
Epoch 10/30
59/59 - 1s - loss: 0.0630 - mae: 38954.5586 - val_loss: 0.1135 - val_mae: 63368.8555 - lr: 0.0100 - 562ms/epoch - 10ms/step
Epoch 11/30
59/59 - 1s - loss: 0.0592 - mae: 37092.7109 - val_loss: 0.0756 - val_mae: 43168.1914 - lr: 0.0100 - 667ms/epoch - 11ms/step
Epoch 12/30
59/59 - 1s - loss: 0.0564 - mae: 36305.6523 - val_loss: 0.0539 - val_mae: 36463.4414 - lr: 0.0100 - 725ms/epoch - 12ms/step
Epoch 13/30
59/59 - 1s - loss: 0.0131 - mae: 14490.8447 - val_loss: 0.0183 - val_mae: 15141.9609 - lr: 0.0020 - 606ms/epoch - 10ms/step
Epoch 14/30
59/59 - 1s - loss: 0.0108 - mae: 13287.9570 - val_loss: 0.0229 - val_mae: 18301.9277 - lr: 0.0020 - 861ms/epoch - 15ms/step
Epoch 15/30
59/59 - 1s - loss: 0.0093 - mae: 12609.0977 - val_loss: 0.0178 - val_mae: 14599.4482 - lr: 0.0020 - 623ms/epoch - 11ms/step
Epoch 16/30
59/59 - 1s - loss: 0.0093 - mae: 12647.4199 - val_loss: 0.0243 - val_mae: 19336.5898 - lr: 0.0020 - 605ms/epoch - 10ms/step
Epoch 17/30
59/59 - 1s - loss: 0.0085 - mae: 12090.3691 - val_loss: 0.0217 - val_mae: 16738.5273 - lr: 0.0020 - 575ms/epoch - 10ms/step
Epoch 18/30
59/59 - 1s - loss: 0.0086 - mae: 12272.2314 - val_loss: 0.0237 - val_mae: 19321.1289 - lr: 0.0020 - 574ms/epoch - 10ms/step
Epoch 19/30
59/59 - 1s - loss: 0.0077 - mae: 11642.5586 - val_loss: 0.0188 - val_mae: 14671.7715 - lr: 0.0020 - 573ms/epoch - 10ms/step
Epoch 20/30
59/59 - 1s - loss: 0.0057 - mae: 9591.2090 - val_loss: 0.0188 - val_mae: 14833.0439 - lr: 4.0000e-04 - 574ms/epoch - 10ms/step
Epoch 21/30
59/59 - 1s - loss: 0.0056 - mae: 9495.5127 - val_loss: 0.0185 - val_mae: 14587.7715 - lr: 4.0000e-04 - 569ms/epoch - 10ms/step
Epoch 22/30
59/59 - 1s - loss: 0.0053 - mae: 9407.4951 - val_loss: 0.0186 - val_mae: 14563.4980 - lr: 4.0000e-04 - 571ms/epoch - 10ms/step
Epoch 23/30
59/59 - 1s - loss: 0.0053 - mae: 9368.8047 - val_loss: 0.0187 - val_mae: 14801.7344 - lr: 4.0000e-04 - 568ms/epoch - 10ms/step
Epoch 24/30
59/59 - 1s - loss: 0.0050 - mae: 9056.7705 - val_loss: 0.0186 - val_mae: 14604.1611 - lr: 8.0000e-05 - 561ms/epoch - 10ms/step
Epoch 25/30
59/59 - 1s - loss: 0.0049 - mae: 9000.3135 - val_loss: 0.0186 - val_mae: 14576.3076 - lr: 8.0000e-05 - 567ms/epoch - 10ms/stephistory
Final epoch (plot to see history):
loss: 0.004929
mae: 9,000
val_loss: 0.01858
val_mae: 14,576
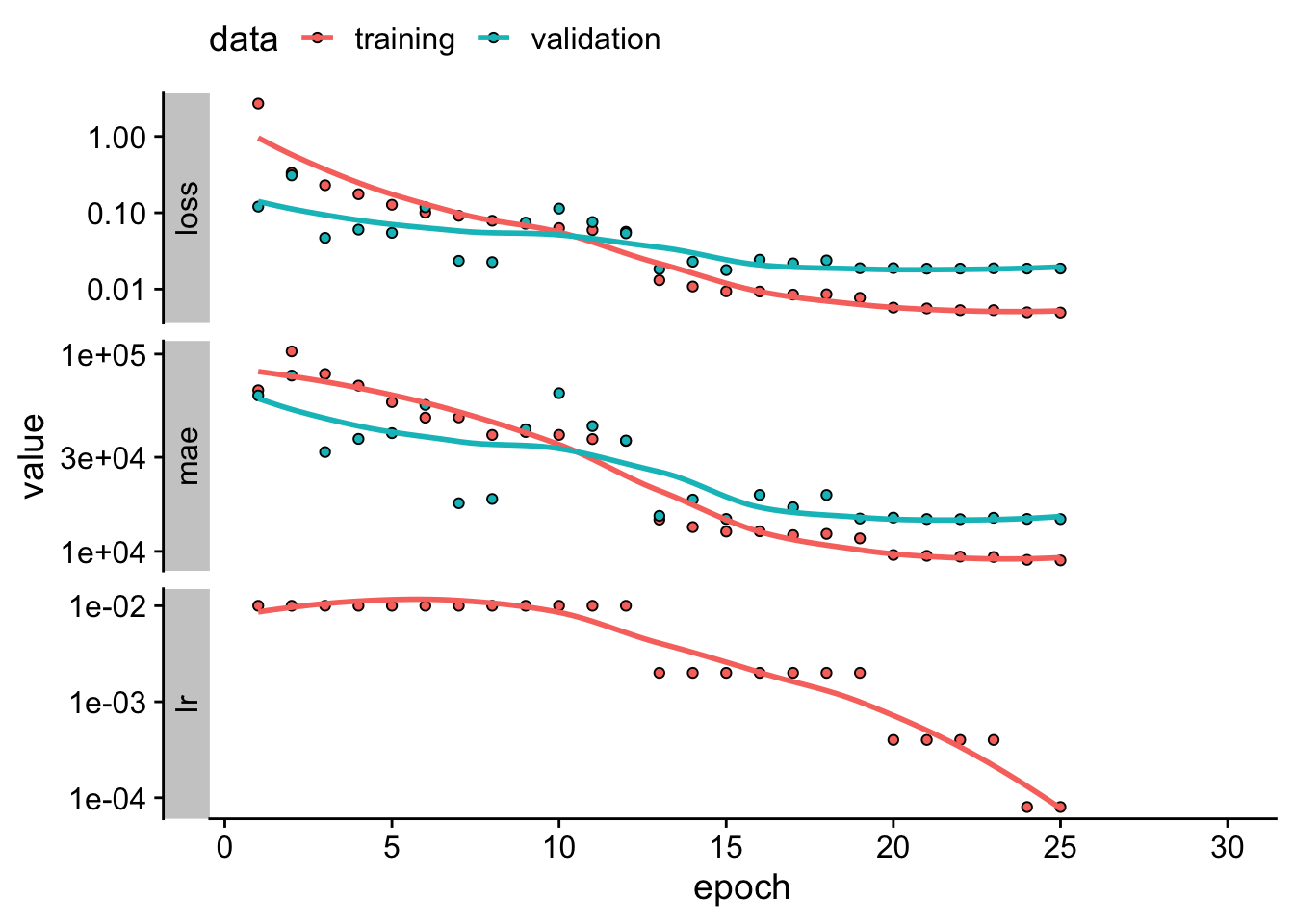
lr: 0.00008 plot(history) +
scale_y_log10() +
theme_cowplot() +
theme(legend.position = "top")